2.4 Polynomials over Finite Fields

Polynomials over finite fields are key to understanding coding theory. They're used to create and analyze error-correcting codes, which are crucial for reliable data transmission. These polynomials have special properties that make them useful in digital communications and cryptography.

In finite fields, polynomials behave differently than in real numbers. Irreducible and primitive polynomials are especially important. They help build finite fields and generate all non-zero elements, which is essential for creating efficient codes and ciphers.

Polynomial Basics

Fundamental Concepts and Properties

Top images from around the web for Fundamental Concepts and Properties

• 

  Methods for Finding Zeros of Polynomials | College Algebra View original

  Is this image relevant?

• 

  End Behavior of Polynomial Functions | College Algebra Corequisite View original

  Is this image relevant?

• 

  7.1 – Algebraic Operations on Polynomials | Hunter College – MATH101 View original

  Is this image relevant?

• 

  Methods for Finding Zeros of Polynomials | College Algebra View original

  Is this image relevant?

• 

  End Behavior of Polynomial Functions | College Algebra Corequisite View original

  Is this image relevant?

1 of 3

Top images from around the web for Fundamental Concepts and Properties

• 

  Methods for Finding Zeros of Polynomials | College Algebra View original

  Is this image relevant?

• 

  End Behavior of Polynomial Functions | College Algebra Corequisite View original

  Is this image relevant?

• 

  7.1 – Algebraic Operations on Polynomials | Hunter College – MATH101 View original

  Is this image relevant?

• 

  Methods for Finding Zeros of Polynomials | College Algebra View original

  Is this image relevant?

• 

  End Behavior of Polynomial Functions | College Algebra Corequisite View original

  Is this image relevant?

1 of 3

• Polynomial ring consists of polynomials with coefficients from a particular field or ring
• Polynomials in the ring can be added, subtracted, and multiplied according to the usual rules of polynomial arithmetic
• Degree of a polynomial refers to the highest power of the variable in the polynomial
  • Polynomials of degree 0 are constant polynomials
  • Linear polynomials have degree 1 ($ax + b$)
  • Quadratic polynomials have degree 2 ($ax^2 + bx + c$)
• Roots of a polynomial are the values of the variable that make the polynomial equal to zero
  • Roots can be found by factoring the polynomial or using techniques like the quadratic formula ($x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ for quadratic polynomials)

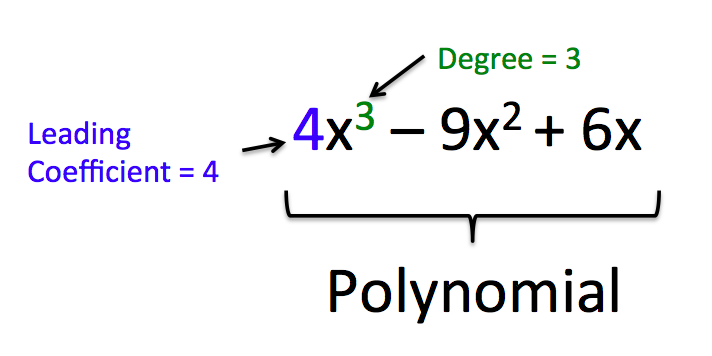
Factorization and Decomposition

• Factorization involves expressing a polynomial as a product of lower-degree polynomials
  • Factoring can reveal the roots of the polynomial (values that make the polynomial equal to zero)
  • Example: $x^2 - 4 = (x - 2)(x + 2)$, roots are $x = 2$ and $x = -2$
• Polynomials can be factored over various fields or rings
  • Factorization over the real numbers may differ from factorization over a finite field
• Polynomials that cannot be factored into lower-degree polynomials are called irreducible polynomials
  • Irreducible polynomials play a crucial role in constructing finite fields and studying their properties

Types of Polynomials

Irreducible and Primitive Polynomials

• Irreducible polynomial cannot be factored into lower-degree polynomials over a given field
  • Analogous to prime numbers in the integers
  • Example: $x^2 + 1$ is irreducible over the real numbers but factors as $(x + i)(x - i)$ over the complex numbers
• Primitive polynomial is a special type of irreducible polynomial
  • Generates all non-zero elements of a finite field when used as the modulus for polynomial arithmetic
  • Example: $x^4 + x + 1$ is a primitive polynomial over GF(2) (binary field)

Cyclotomic and Minimal Polynomials

• Cyclotomic polynomial $\Phi_n(x)$ is the polynomial whose roots are the primitive $n$-th roots of unity
  • Primitive $n$-th roots of unity are complex numbers $z$ satisfying $z^n = 1$ and $z^k \neq 1$ for $0 < k < n$
  • Example: $\Phi_4(x) = x^2 + 1$ has roots $i$ and $-i$, which are the primitive 4th roots of unity
• Minimal polynomial of an element $\alpha$ over a field $F$ is the monic polynomial $p(x)$ of lowest degree such that $p(\alpha) = 0$
  • Minimal polynomials are always irreducible over the base field
  • Example: Minimal polynomial of $\sqrt{2}$ over the rational numbers is $x^2 - 2$