
U-Substitution
3 min read•november 15, 2021
Rupi Adhikary
Rupi Adhikary
⚡️Watch: AP Calculus AB/BC - Integration by Substitution
U-sub, also known as integration by substitution, is one of the key components of integrals. Chances are, you've come across an integral like the one below and been completely lost on where to start.
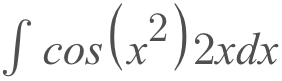
Fear not! In this article, we'll go over what U-Sub is and how and when you should use it! For the sake of learning the concept first, all of the examples we're going to be using will be indefinite integrals.
Let's jump right into it then!
Before using u-sub, you want to be able to write your integral as
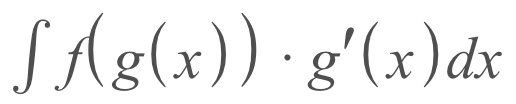
Key Components
If we look at the function above, there are a couple things that we should take note of
- f(x) - this would be represented as cos(x) in the example
- f(g(x)) - in the example, this would be cos(x^2)
- g(x) - the 'x' of 'f(x)', in the example at the top of this article, this would be x^2
- g'(x) - the derivative of g(x), in the example, this would be 2x

Why U-Sub?
U-substitution is all about making taking the integral of a function easier. To do this, we need to substitute a part of the function with 'u' so we can be left with something easier to work with.
We substitute g(x), with the term 'u'. This means that the derivative of g(x) changes as well. G'(x) becomes the derivative of 'u' or 'du'.
This example is perfect because we can clearly see what the derivative of g(x) is but it doesn't always work out so easily. To ensure that you're correctly finding g'(x), simply take the derivative of g(x).
In the case of the example, this would play out something like this
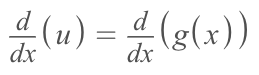

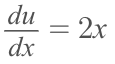
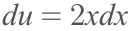
Now that we have 'u' and 'du', we can substitute them into our original integral (remember, the original integral was the integral of cos(x^2) * 2x dx).
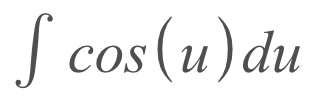
Next, all we have to do is take the integral in terms of 'u', which basically just means taking the integral but instead of 'x' as you would usually put, 'u' would take its place.
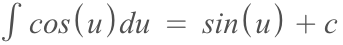
Our last step is to substitute back in g(x) for 'u'.
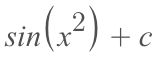
What if it isn't so pretty?
While this example worked out pretty well, as mentioned before, the majority of the integrals you're going to be taking won't. This means that it might take a little bit of extra work getting the integral into this type of format
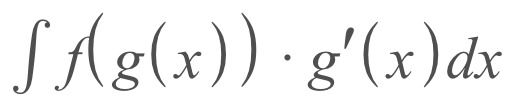
Say, we have the another integral like the one below
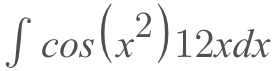
It looks very similar to the one that we just worked with! The only problem, is that pesky '12x'. So, how do we go about solving this?
We're going to go through the same steps that we did last time.
- What is our g(x)? x^2
- What is our f(x)? cos(x)
- What is our f(g(x))? cos(x^2)
- What is g'(x)? 2x
We see that everything matches up except g'(x). 12x is simply 2x multiplied by 6 right? So, if we use the rule of constants we can pull that 6 up front and be left with the 2x we need.
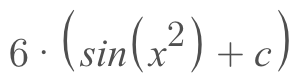
Now, we can take the integral as usual, but make sure not to forget about the 6 we took out!
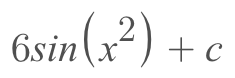
And that's it! Now you know how to use u-sub like a pro! If you need some extra help and practice with this concept check out these awesome links too!
Practice and help with u-sub!
- https://www.mathsisfun.com/calculus/integration-by-substitution.html
- https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-9/a/review-applying-u-substitution
- http://tutorial.math.lamar.edu/Classes/CalcI/SubstitutionRuleIndefinite.aspx
- https://www.math.hmc.edu/calculus/tutorials/substitution/
- https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-9/e/integration-by-u-substitution
U-Substitution
3 min read•november 15, 2021
Rupi Adhikary
Rupi Adhikary
⚡️Watch: AP Calculus AB/BC - Integration by Substitution
U-sub, also known as integration by substitution, is one of the key components of integrals. Chances are, you've come across an integral like the one below and been completely lost on where to start.
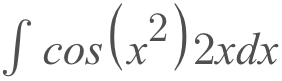
Fear not! In this article, we'll go over what U-Sub is and how and when you should use it! For the sake of learning the concept first, all of the examples we're going to be using will be indefinite integrals.
Let's jump right into it then!
Before using u-sub, you want to be able to write your integral as
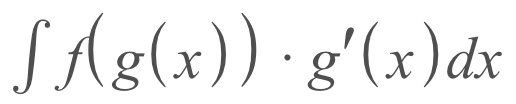
Key Components
If we look at the function above, there are a couple things that we should take note of
- f(x) - this would be represented as cos(x) in the example
- f(g(x)) - in the example, this would be cos(x^2)
- g(x) - the 'x' of 'f(x)', in the example at the top of this article, this would be x^2
- g'(x) - the derivative of g(x), in the example, this would be 2x

Why U-Sub?
U-substitution is all about making taking the integral of a function easier. To do this, we need to substitute a part of the function with 'u' so we can be left with something easier to work with.
We substitute g(x), with the term 'u'. This means that the derivative of g(x) changes as well. G'(x) becomes the derivative of 'u' or 'du'.
This example is perfect because we can clearly see what the derivative of g(x) is but it doesn't always work out so easily. To ensure that you're correctly finding g'(x), simply take the derivative of g(x).
In the case of the example, this would play out something like this
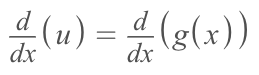

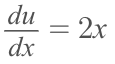
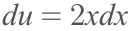
Now that we have 'u' and 'du', we can substitute them into our original integral (remember, the original integral was the integral of cos(x^2) * 2x dx).
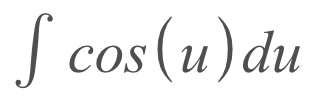
Next, all we have to do is take the integral in terms of 'u', which basically just means taking the integral but instead of 'x' as you would usually put, 'u' would take its place.
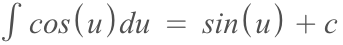
Our last step is to substitute back in g(x) for 'u'.
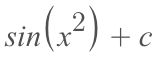
What if it isn't so pretty?
While this example worked out pretty well, as mentioned before, the majority of the integrals you're going to be taking won't. This means that it might take a little bit of extra work getting the integral into this type of format
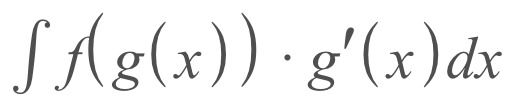
Say, we have the another integral like the one below
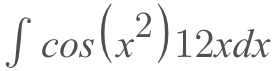
It looks very similar to the one that we just worked with! The only problem, is that pesky '12x'. So, how do we go about solving this?
We're going to go through the same steps that we did last time.
- What is our g(x)? x^2
- What is our f(x)? cos(x)
- What is our f(g(x))? cos(x^2)
- What is g'(x)? 2x
We see that everything matches up except g'(x). 12x is simply 2x multiplied by 6 right? So, if we use the rule of constants we can pull that 6 up front and be left with the 2x we need.
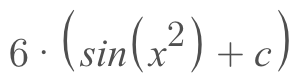
Now, we can take the integral as usual, but make sure not to forget about the 6 we took out!
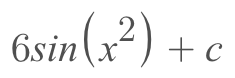
And that's it! Now you know how to use u-sub like a pro! If you need some extra help and practice with this concept check out these awesome links too!
Practice and help with u-sub!
- https://www.mathsisfun.com/calculus/integration-by-substitution.html
- https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-9/a/review-applying-u-substitution
- http://tutorial.math.lamar.edu/Classes/CalcI/SubstitutionRuleIndefinite.aspx
- https://www.math.hmc.edu/calculus/tutorials/substitution/
- https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-9/e/integration-by-u-substitution

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.