Glossary

18.1 Kernel Density Estimation

4 min read•august 9, 2024

is a powerful nonparametric method for estimating probability distributions. It uses data points and kernel functions to create smooth, continuous estimates of underlying distributions, offering advantages over traditional histograms.

's flexibility comes with challenges in choosing optimal bandwidths and kernel functions. Understanding these trade-offs is crucial for accurate , making KDE a valuable tool in the broader context of nonparametric methods and resampling techniques.

Kernel Density Estimation Basics

Nonparametric Density Estimation and Kernel Functions

Top images from around the web for Nonparametric Density Estimation and Kernel Functions

  • 核密度估计 Kernel Density Estimation(KDE)_南极企鹅-CSDN博客_kernel density estimation View original

    Is this image relevant?

  • Kernel Density Estimation [The Hundred-Page Machine Learning Book] View original

    Is this image relevant?

  • 核密度估计 Kernel Density Estimation(KDE)_南极企鹅-CSDN博客_kernel density estimation View original

    Is this image relevant?

1 of 3

Top images from around the web for Nonparametric Density Estimation and Kernel Functions

  • 核密度估计 Kernel Density Estimation(KDE)_南极企鹅-CSDN博客_kernel density estimation View original

    Is this image relevant?

  • Kernel Density Estimation [The Hundred-Page Machine Learning Book] View original

    Is this image relevant?

  • 核密度估计 Kernel Density Estimation(KDE)_南极企鹅-CSDN博客_kernel density estimation View original

    Is this image relevant?

1 of 3
  • Kernel Density Estimation (KDE) provides a nonparametric approach to estimate probability density functions
  • Utilizes observed data points to construct a smooth, continuous estimate of the underlying distribution
  • Kernel function acts as a weighting function centered at each data point
  • Common kernel functions include Gaussian, Epanechnikov, and triangular kernels
  • KDE formula: f^h(x)=1nh∑i=1nK(x−Xih)\hat{f}_h(x) = \frac{1}{nh} \sum_{i=1}^n K\left(\frac{x - X_i}{h}\right)
    • f^h(x)\hat{f}_h(x) represents the estimated density at point xx
    • nn denotes the number of data points
    • hh signifies the
    • KK symbolizes the chosen kernel function
  • Kernel functions must be symmetric and integrate to 1

Bandwidth and Smoothing Parameter

  • Bandwidth (h) controls the smoothness of the resulting density estimate
  • Larger bandwidth values produce smoother estimates but may obscure important features
  • Smaller bandwidth values capture more local variations but can lead to overfitting
  • Optimal bandwidth selection balances bias and variance
  • Rule-of-thumb bandwidth estimators (Silverman's rule) provide quick approximations
  • Silverman's rule for Gaussian kernels: h=0.9min⁡(σ,IQR1.34)n−1/5h = 0.9 \min(\sigma, \frac{IQR}{1.34}) n^{-1/5}
    • σ\sigma represents the standard deviation of the data
    • IQRIQR denotes the interquartile range

Bias-Variance Tradeoff in KDE

  • Bias refers to the systematic error in the estimate
  • Variance measures the variability of the estimate across different samples
  • Small bandwidth leads to low bias but high variance (undersmoothing)
  • Large bandwidth results in high bias but low variance (oversmoothing)
  • Optimal bandwidth minimizes the (MISE)
  • MISE combines both bias and variance: MISE=E[∫(f^(x)−f(x))2dx]MISE = E[\int (\hat{f}(x) - f(x))^2 dx]
  • techniques help find the optimal bandwidth by minimizing error estimates

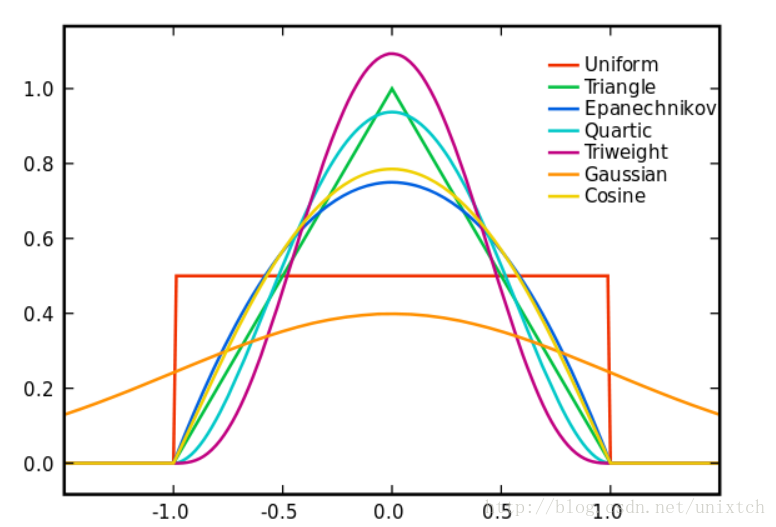
Types of Kernels

Common Kernel Functions

  • maximizes efficiency in terms of
  • Epanechnikov kernel function: K(u)=34(1−u2) for ∣u∣≤1, 0 otherwiseK(u) = \frac{3}{4}(1-u^2) \text{ for } |u| \leq 1, \text{ 0 otherwise}
  • offers smooth estimates and mathematical convenience
  • Gaussian kernel function: K(u)=12πe−12u2K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}u^2}
  • provides a simple, computationally efficient option
  • Triangular kernel function: K(u)=(1−∣u∣) for ∣u∣≤1, 0 otherwiseK(u) = (1 - |u|) \text{ for } |u| \leq 1, \text{ 0 otherwise}
  • assigns equal weight within a fixed range
  • Uniform kernel function: K(u)=12 for ∣u∣≤1, 0 otherwiseK(u) = \frac{1}{2} \text{ for } |u| \leq 1, \text{ 0 otherwise}

Comparison of KDE with Histogram

  • Histograms divide data into discrete bins, while KDE produces a continuous estimate
  • KDE overcomes the discontinuity issues present in histograms
  • Histogram bin width corresponds to KDE bandwidth
  • KDE offers better smoothness and differentiability compared to histograms
  • Histograms can be sensitive to bin width and starting point choices
  • KDE provides more consistent results across different samples
  • Computational complexity: histograms O(n), KDE O(n^2) (naive implementation)
  • KDE allows for easier interpretation of multimodal distributions

Advanced KDE Techniques

Multivariate Kernel Density Estimation

  • Extends KDE to estimate joint probability densities in multiple dimensions
  • Multivariate KDE formula: f^H(x)=1n∑i=1nKH(x−Xi)\hat{f}_H(x) = \frac{1}{n} \sum_{i=1}^n K_H(x - X_i)
    • HH represents the bandwidth matrix
    • KH(x)=∣H∣−1/2K(H−1/2x)K_H(x) = |H|^{-1/2} K(H^{-1/2}x)
  • Bandwidth selection becomes more challenging in higher dimensions
  • Curse of dimensionality affects the accuracy of estimates as dimensions increase
  • Product kernels use separate bandwidths for each dimension
  • Spherical kernels apply the same bandwidth in all dimensions

Boundary Correction and Adaptive KDE

  • occurs when estimating densities near the edges of the support
  • mitigates boundary bias by reflecting data points across boundaries
  • Boundary kernel methods adapt the kernel shape near boundaries
  • adjusts bandwidth based on local data density
  • guides the selection of local bandwidths
  • Adaptive KDE formula: f^(x)=1n∑i=1n1h(Xi)K(x−Xih(Xi))\hat{f}(x) = \frac{1}{n} \sum_{i=1}^n \frac{1}{h(X_i)} K\left(\frac{x - X_i}{h(X_i)}\right)
    • h(Xi)h(X_i) denotes the local bandwidth at point XiX_i

Cross-validation for Bandwidth Selection

  • (LOOCV) assesses the quality of bandwidth choices
  • LOOCV criterion: CV(h)=1n∑i=1nlog⁡f^−i(Xi)CV(h) = \frac{1}{n} \sum_{i=1}^n \log \hat{f}_{-i}(X_i)
    • f^−i(Xi)\hat{f}_{-i}(X_i) represents the density estimate at XiX_i without using XiX_i
  • maximizes the log-likelihood of the density estimate
  • minimizes the integrated squared error
  • Grid search or optimization algorithms find the bandwidth minimizing the CV criterion
  • K-fold cross-validation offers a computationally efficient alternative to LOOCV
  • Plug-in methods estimate optimal bandwidth using asymptotic approximations

Key Terms to Review (30)

Adaptive KDE: Adaptive Kernel Density Estimation (Adaptive KDE) is a statistical technique used to estimate the probability density function of a random variable by adjusting the bandwidth of the kernel function based on the local density of data points. This method improves the estimation by allowing for variable smoothing, where areas with higher data concentration receive a smaller bandwidth for finer detail, while sparser areas use a larger bandwidth to avoid oversmoothing.
B. W. Silverman: B. W. Silverman is a prominent statistician known for his contributions to non-parametric statistics and, particularly, kernel density estimation (KDE). His work has provided foundational insights into the development and implementation of KDE, a technique used to estimate the probability density function of a random variable. By addressing issues such as bandwidth selection, Silverman has significantly influenced how statisticians and data scientists apply kernel methods in practical scenarios.
Bandwidth: Bandwidth refers to the width of the interval that is used in smoothing data, specifically in Kernel Density Estimation (KDE). It plays a critical role in determining the level of detail in the density estimate; a larger bandwidth produces a smoother estimate but may overlook finer details, while a smaller bandwidth captures more detail but can introduce noise.
Bias-Variance Tradeoff: The bias-variance tradeoff is a fundamental concept in machine learning and statistics that describes the balance between two sources of error that affect model performance: bias, which refers to the error due to overly simplistic assumptions in the learning algorithm, and variance, which refers to the error due to excessive sensitivity to fluctuations in the training data. Understanding this tradeoff is crucial for building models that generalize well to unseen data while avoiding both underfitting and overfitting.
Boundary Bias: Boundary bias refers to the systematic error that occurs in kernel density estimation when data points are near the boundaries of the support of the distribution. This bias arises because the kernel functions used to estimate the density may not adequately account for the limited available data at the boundaries, leading to underestimation or overestimation of the density in those regions. Understanding boundary bias is crucial for accurate statistical modeling and inference, especially when dealing with data that is confined within specific limits.
Cross-validation: Cross-validation is a statistical technique used to assess how the results of a predictive model will generalize to an independent data set. It is particularly useful in situations where the goal is to prevent overfitting, ensuring that the model performs well not just on training data but also on unseen data, which is vital for accurate predictions and insights.
David W. Scott: David W. Scott is a prominent statistician known for his contributions to kernel density estimation, a non-parametric way to estimate the probability density function of a random variable. His work has significantly advanced the understanding and application of smoothing techniques in data analysis, making it easier to visualize data distributions and identify patterns without assuming a specific underlying distribution.
Density Estimation: Density estimation is a statistical technique used to estimate the probability density function of a random variable based on observed data. This method allows researchers to understand the underlying distribution of data points without making strong assumptions about the form of the distribution. It plays a crucial role in non-parametric statistics, where the focus is on drawing conclusions from data without predefined models.
Epanechnikov Kernel: The Epanechnikov kernel is a specific type of kernel function used in kernel density estimation that is defined by a parabolic shape. This kernel is significant because it minimizes the mean integrated squared error, making it one of the most efficient choices for estimating probability density functions. It provides a smooth estimate of the underlying distribution while balancing bias and variance effectively.
Gaussian kernel: A gaussian kernel is a function used in various statistical applications, including kernel density estimation, that represents a smooth, bell-shaped curve based on the Gaussian distribution. This kernel is particularly valued for its ability to provide a continuous and differentiable estimation of probability density functions, making it useful in non-parametric statistics. It helps in estimating the underlying distribution of data points by weighting nearby observations more heavily than those farther away.
H for bandwidth: In the context of kernel density estimation, 'h' represents the bandwidth, a crucial parameter that determines the smoothness of the estimated density function. The value of 'h' affects how closely the kernel function follows the data points, influencing the balance between bias and variance in the estimation process. A smaller bandwidth leads to a more sensitive estimate that captures finer details, while a larger bandwidth results in a smoother estimate that may overlook important features.
Integral equals one: The term 'integral equals one' refers to the property that the total area under a probability density function (PDF) must equal one. This characteristic ensures that the probabilities of all possible outcomes sum to 1, making it a fundamental aspect of probability distributions and crucial for correctly interpreting data within statistics.
K(x): In the context of kernel density estimation, k(x) represents the kernel function applied to the data point x, which is used to estimate the probability density function of a random variable. This function plays a crucial role in determining how much influence each data point has on the estimated density at any given location, effectively smoothing the distribution of data points. The choice of kernel function and its bandwidth directly affects the accuracy and visual representation of the resulting density estimate.
Kde: KDE, or Kernel Density Estimation, is a non-parametric way to estimate the probability density function of a random variable. It provides a smooth estimate of the distribution of data points by placing a kernel function on each data point and summing these to obtain a continuous curve. This method is particularly useful for visualizing the underlying distribution of data without assuming any specific parametric form.
Kernel Density Estimation: Kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. It allows for the visualization of the distribution of data points by smoothing out the observed values using a kernel function, providing an insightful alternative to histograms for understanding data distributions.
Least squares cross-validation: Least squares cross-validation is a statistical technique used to assess the predictive performance of a model by dividing data into subsets, fitting the model to some subsets, and validating it on the remaining data. This method helps in determining the optimal parameters for a model, particularly in scenarios where overfitting may occur. It is essential for ensuring that the model generalizes well to unseen data and does not just perform well on the training dataset.
Leave-one-out cross-validation: Leave-one-out cross-validation (LOOCV) is a specific type of cross-validation where a single observation is used as the validation set, while the remaining observations form the training set. This method is particularly useful for assessing how well a model will generalize to an independent dataset, especially when the amount of data is limited. LOOCV helps to ensure that every single data point is used for both training and validation, providing a robust estimate of the model's performance.
Likelihood cross-validation: Likelihood cross-validation is a technique used to assess the performance of statistical models by measuring how well a model predicts a set of data points, using the likelihood function as a criterion. This method helps in selecting the best model by comparing the likelihoods of different models on validation data, thereby providing a more nuanced understanding of model fit and performance.
Mean Integrated Squared Error: Mean Integrated Squared Error (MISE) is a measure used to assess the performance of an estimator, particularly in non-parametric statistics, by evaluating the average squared difference between the estimated density function and the true density function across a specified domain. It provides insight into how well the estimator approximates the underlying distribution, making it crucial in contexts like kernel density estimation where accurate density estimation is essential for data analysis and interpretation.
Mean Squared Error: Mean squared error (MSE) is a measure used to evaluate the accuracy of a predictive model by calculating the average squared difference between the estimated values and the actual values. It serves as a crucial metric for understanding how well a model performs, guiding decisions on model selection and refinement. By assessing the errors made by predictions, MSE helps highlight the balance between bias and variance, as well as the effectiveness of techniques like regularization and variable selection.
Multivariate distribution: A multivariate distribution describes the probability distribution of multiple random variables at the same time. This concept allows for understanding the relationships and dependencies between these variables, providing a more comprehensive view than analyzing each variable individually. It encompasses various forms, including joint, marginal, and conditional distributions, which help in modeling complex data scenarios.
Non-negativity: Non-negativity refers to the property that a value cannot be less than zero, indicating that it is either positive or zero. This concept is fundamental in various fields, especially in probability and statistics, as it ensures that certain quantities, like probabilities or density estimates, remain valid and meaningful. Non-negativity plays a critical role in ensuring that the sum of probabilities equals one and that density functions reflect true likelihoods without suggesting impossible scenarios.
Pilot Density Estimate: A pilot density estimate is an initial, rough estimation of the underlying probability density function of a dataset, often used in the context of kernel density estimation. This preliminary estimate helps in selecting the appropriate bandwidth and kernel function for more refined density estimation. It provides a quick glimpse into the shape of the data distribution, guiding subsequent analysis and adjustments.
Plug-in Selector: A plug-in selector is a method used in statistical analysis to choose the bandwidth parameter in kernel density estimation. This technique is essential as it directly affects the smoothness and accuracy of the estimated density function, impacting the overall representation of the data. By optimizing this selection process, plug-in selectors aim to minimize the integrated squared error between the true underlying distribution and the estimated density.
Probability Density Function: A probability density function (PDF) is a function that describes the likelihood of a continuous random variable taking on a particular value. Unlike discrete variables, where probabilities are assigned to specific outcomes, the PDF gives the relative likelihood of outcomes in a continuous space and is essential for calculating probabilities over intervals. The area under the PDF curve represents the total probability of the random variable, which must equal one.
Reflection Method: The reflection method is a technique used in statistics, particularly in kernel density estimation, to address boundary issues in data. This method involves reflecting the data across a boundary to create a more comprehensive estimation of the probability density function, thereby improving the accuracy of density estimates near the edges of the data range.
Smoothing: Smoothing is a statistical technique used to create a smooth curve from a set of data points, which helps in revealing the underlying structure or pattern within the data. This approach reduces noise and fluctuations in the data, making it easier to analyze trends or distributions. Smoothing is particularly beneficial in scenarios where the data is irregular or has high variability, as it allows for clearer insights into the overall behavior of the dataset.
Triangular kernel: A triangular kernel is a type of kernel function used in kernel density estimation that has a linear shape, resembling a triangle. It assigns weights to data points based on their distance from a central point, decreasing linearly from the peak to the edges, which allows for smoother estimates of probability density functions. This kernel is particularly effective for capturing local variations in data while being simple and computationally efficient.
Uniform Kernel: A uniform kernel is a type of kernel function used in kernel density estimation that assigns equal weight to all points within a specified bandwidth. This method creates a smooth estimate of the probability density function, providing a simplistic way to visualize the underlying distribution of data. The uniform kernel is particularly useful for generating a straightforward, unbiased estimate without introducing additional complexity from varying weights across the data range.
Univariate Distribution: A univariate distribution describes the probability distribution of a single random variable, focusing on how values are distributed across its range. This type of distribution provides essential insights into the characteristics of the variable, such as its central tendency, variability, and shape. Understanding univariate distributions is crucial for various statistical analyses, as it lays the groundwork for more complex analyses involving multiple variables.
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
Back
Practice QuizGlossary
Practice QuizGlossary
Next guide