Glossary

5.2 Secant Method: Derivation and Implementation

3 min read•august 1, 2024

The is a powerful tool for solving nonlinear equations without needing derivatives. It's like 's cool cousin, using two points to estimate the slope instead of calculus. This approach makes it super handy for tricky functions.

While it's not as fast as Newton's Method near the solution, the Secant Method shines when derivatives are a pain to calculate. It's a great balance of speed and simplicity, making it a go-to choice for many real-world problems.

Secant Method Derivation

Fundamental Concepts and Approach

Top images from around the web for Fundamental Concepts and Approach

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

1 of 3

Top images from around the web for Fundamental Concepts and Approach

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

  • The Derivative – Quantitative Analysis for Business View original

    Is this image relevant?

1 of 3
  • Secant method solves nonlinear equations of the form f(x)=0f(x) = 0 using iterative
  • Approximates derivative using eliminating explicit derivative calculations
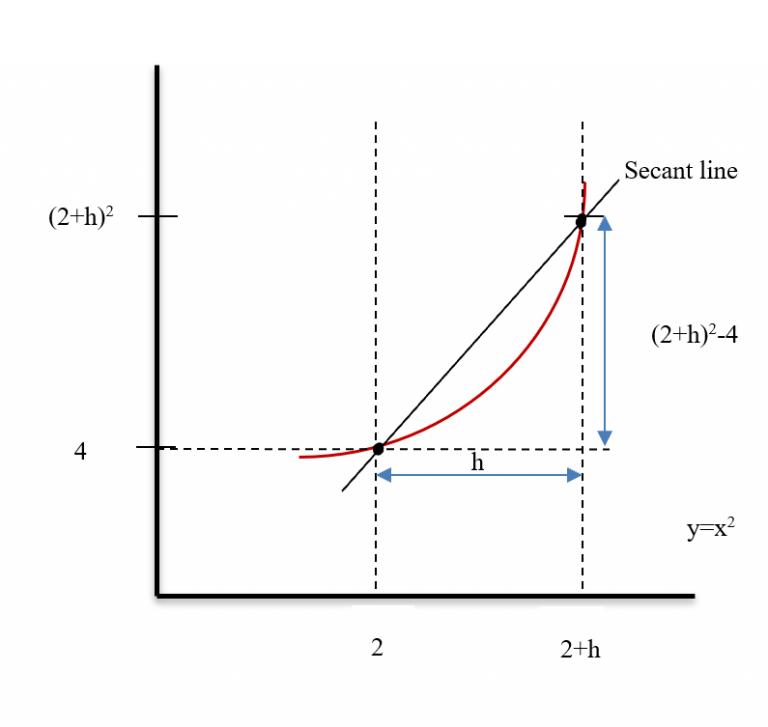
  • Begins with general form of Newton's method xn+1=xn−f(xn)f′(xn)x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
  • Replaces derivative f′(xn)f'(x_n) with approximation f(xn)−f(xn−1)xn−xn−1\frac{f(x_n) - f(x_{n-1})}{x_n - x_{n-1}}
  • Results in iterative formula xn+1=xn−f(xn)xn−xn−1f(xn)−f(xn−1)x_{n+1} = x_n - f(x_n) \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})}

Convergence and Error Analysis

  • Convergence superlinear with order approximately 1.618 (golden ratio)
  • expressed as ∣en+1∣≈C∣en∣∣en−1∣|e_{n+1}| \approx C|e_n||e_{n-1}| (C constant, ene_n error at nth iteration)
  • Converges faster than linear methods (bisection) but slower than quadratic methods (Newton's)
  • Error reduction factor changes each iteration unlike

Secant Method Implementation

Algorithm Structure and Initialization

  • Requires two x0x_0 and x1x_1 to start iterative process
  • Implement based on function value tolerance or consecutive approximation difference
  • Include safeguards against when calculating finite difference approximation
  • Implement for non-convergence within specified maximum iterations
  • Structure algorithm for easy modification of function and initial guesses
  • Example initialization: 
    def secant_method(f, x0, x1, tol=1e-6, max_iter=100):
    for i in range(max_iter):
        fx0, fx1 = f(x0), f(x1)
        if abs(fx1) < tol:
            return x1
        if fx0 == fx1:
            raise ValueError("Division by zero encountered")
        x_new = x1 - fx1 * (x1 - x0) / (fx1 - fx0)
        x0, x1 = x1, x_new
    raise ValueError("Method did not converge")

Optimization and Numerical Considerations

  • Minimize using appropriate data structures for intermediate results
  • Use instead of absolute error for stopping criterion enhancing numerical stability
  • Implement to improve convergence in challenging regions
  • Consider using for sensitive problems
  • Employ techniques like bracketing to ensure method stays within desired solution range

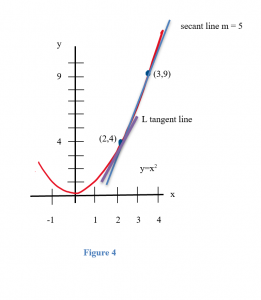
Secant vs Newton Methods

Computational Efficiency

  • Secant method requires only function evaluations while Newton's needs function and derivative calculations
  • Secant method often requires fewer function evaluations per iteration potentially leading to faster overall performance
  • Newton's method converges more rapidly when close to root but secant may be more robust when starting farther from solution
  • Secant method advantageous when derivative difficult or expensive to compute (, )

Convergence Characteristics

  • Secant method has lower convergence order (≈1.618) compared to Newton's method (quadratic, order 2)
  • Both methods can suffer from divergence or oscillation around root depending on function and initial guesses
  • Newton's method sensitive to derivative behavior while secant method more stable when derivative approaches zero near root
  • Secant method may struggle with functions having discontinuities or sharp turns near root

Secant Method Advantages and Limitations

Advantages

  • Does not require explicit derivative calculations beneficial for complex functions or
  • Potentially fewer function evaluations per iteration improving efficiency for computationally expensive functions
  • More stable than Newton's method when derivative approaches zero near root (avoiding division by small numbers)
  • Useful for problems where derivative unavailable difficult to compute or computationally expensive (finite element analysis, )

Limitations

  • Needs two initial guesses affecting convergence if poorly chosen
  • May converge more slowly than Newton's method especially when very close to root
  • Can fail to converge for functions with or complex behavior near root (fractal boundaries, highly oscillatory functions)
  • May struggle with functions having discontinuities or sharp turns near root (piecewise functions, absolute value functions)
  • Can exhibit erratic behavior or diverge if initial guesses too far from actual root
  • Sensitive to rounding errors in finite difference approximation potentially affecting accuracy in some cases

Key Terms to Review (25)

Adaptive Step Size: Adaptive step size refers to the technique used in numerical methods where the step size is adjusted dynamically based on the behavior of the solution being computed. This approach helps improve accuracy and efficiency by allowing smaller step sizes when the solution changes rapidly and larger step sizes when the solution is smoother. It is particularly relevant in methods that solve ordinary differential equations and in iterative approaches that seek roots or solutions.
Bisection Method: The bisection method is a root-finding technique that repeatedly bisects an interval to hone in on a root of a continuous function. This method is based on the Intermediate Value Theorem, ensuring that if a function changes sign over an interval, there is at least one root within that interval. It connects with various concepts like algorithms for numerical methods, understanding error and convergence rates, and serves as a foundational approach before exploring more complex methods.
Black-box systems: Black-box systems refer to processes or models where the internal workings are not known or are not accessible for analysis; only the input and output can be observed. This concept is crucial in numerical methods because it allows us to use algorithms like the secant method without needing to understand the underlying function completely. It emphasizes that as long as we can get outputs from given inputs, we can approximate solutions effectively without delving into the details of how those outputs are generated.
Bracketing Techniques: Bracketing techniques are numerical methods used to find roots of equations by enclosing the root within two points, ensuring that a sign change occurs between them. These methods are essential for identifying intervals in which the function changes its sign, indicating the presence of a root according to the Intermediate Value Theorem. They serve as a foundation for more advanced root-finding algorithms, such as the secant method, which builds on the concept of narrowing down the interval where the root lies.
Complex Functions: Complex functions are mathematical functions that take complex numbers as inputs and produce complex numbers as outputs. These functions can be expressed in the form $$f(z) = u(x, y) + iv(x, y)$$, where $$z = x + iy$$, with $$u$$ and $$v$$ being real-valued functions of the real variables $$x$$ and $$y$$. Understanding complex functions is crucial when applying numerical methods to analyze and solve problems that involve equations where traditional real-valued functions may not suffice.
Computational efficiency: Computational efficiency refers to the effectiveness of an algorithm in terms of the resources it consumes, particularly time and space, to produce a desired output. It evaluates how well an algorithm performs relative to its computational cost, which can be crucial in determining the feasibility of numerical methods and software applications. Efficient algorithms can handle larger datasets and more complex calculations while minimizing resource usage, making them essential in areas like optimization, data analysis, and scientific computing.
Convergence Characteristics: Convergence characteristics refer to the behavior of an iterative method as it approaches the solution of an equation. These characteristics determine how quickly and effectively a method converges to a root, which is especially important in numerical methods like the secant method. Understanding these traits helps in analyzing the efficiency and reliability of the method in finding accurate solutions to equations.
Division by Zero: Division by zero occurs when a number is divided by zero, which is mathematically undefined. In the context of numerical methods, encountering division by zero can lead to significant computational issues, especially in iterative methods like the secant method, where division by the difference of two approximations can occur. Understanding this concept is crucial for implementing and analyzing numerical algorithms effectively, as it can impact convergence and lead to erroneous results.
Error Equation: The error equation is a mathematical expression that quantifies the difference between an exact solution and an approximate solution in numerical analysis. This concept is crucial as it helps in assessing the accuracy of iterative methods, like the secant method, by providing a way to measure how close an approximation is to the true value. Understanding the error equation aids in optimizing convergence rates and improving the overall reliability of numerical solutions.
Error Handling: Error handling is the process of anticipating, detecting, and responding to errors that may occur during the execution of a program or algorithm. In numerical methods, particularly with iterative techniques like the Secant Method, effective error handling ensures that users are aware of potential problems such as division by zero or non-convergence, and provides mechanisms to address these issues without crashing or producing incorrect results.
Finite Difference Quotient: A finite difference quotient is an approximation of the derivative of a function using values of the function at discrete points. It provides a way to estimate the rate of change of a function, which is particularly useful in numerical methods for solving equations, such as the secant method. By utilizing finite difference quotients, one can derive formulas that facilitate the approximation of solutions without requiring an explicit form of the function's derivative.
Fixed-Point Iteration: Fixed-point iteration is a numerical method used to find solutions of equations of the form $x = g(x)$, where a function $g$ maps an interval into itself. This technique involves repeatedly applying the function to an initial guess until the results converge to a fixed point, which is the solution of the equation. The success of this method relies on properties such as continuity and the contractive nature of the function, linking it to various numerical concepts and error analysis.
Function evaluations: Function evaluations refer to the process of calculating the output of a mathematical function for specific input values. This concept is crucial in numerical methods, where determining the value of a function at certain points can help find roots or optimize functions, making it especially significant in techniques like the Secant Method, which approximates solutions to equations using successive function evaluations.
Higher Precision Arithmetic: Higher precision arithmetic refers to mathematical calculations that use more digits than standard floating-point representation, allowing for greater accuracy and reduced rounding errors. This is crucial in numerical analysis, particularly when implementing iterative methods like the secant method, where the approximation of roots can be sensitive to precision. Using higher precision helps to ensure that small changes in values do not lead to significant deviations in results, which is essential for converging accurately to a solution.
Initial Guesses: Initial guesses refer to the preliminary estimates or values provided as starting points in iterative methods used for finding roots of equations or optimizing functions. The choice of initial guesses can significantly influence the convergence behavior, accuracy, and efficiency of the method employed, especially in numerical techniques like the secant method. Properly selecting initial guesses is crucial as it affects how quickly and accurately a solution is reached.
Iteration Process: The iteration process is a method used to refine and improve approximations of a solution to a problem through repeated calculations. This technique involves using previous estimates to generate new ones until a desired level of accuracy is achieved. It is fundamental in numerical methods, where it helps in finding roots of equations and optimizing functions.
Multiple roots: Multiple roots refer to the scenario where a particular root of a function appears more than once. This can complicate the process of finding roots, as standard numerical methods may struggle to converge effectively when encountering such roots due to their repeated nature. Understanding multiple roots is crucial for adapting root-finding techniques and ensuring accurate solutions, especially when using methods like the secant method or other root-finding algorithms.
Newton's Method: Newton's Method is an iterative numerical technique used to find approximate solutions to real-valued functions, particularly for finding roots of equations. It leverages the function's derivative to rapidly converge on a solution, making it particularly useful in the context of solving nonlinear equations and optimization problems.
Numerical Simulations: Numerical simulations are computational methods used to model and analyze complex systems by solving mathematical equations approximately. They provide a way to predict the behavior of systems in various fields, allowing researchers and engineers to visualize outcomes, test hypotheses, and optimize designs without needing physical prototypes. These simulations are particularly useful in cases where analytical solutions are difficult or impossible to obtain.
Optimization Problems: Optimization problems are mathematical challenges that involve finding the best solution from a set of feasible solutions, often subject to certain constraints. These problems can appear in various fields, including economics, engineering, and computer science, where the goal is to maximize or minimize a specific objective function. Understanding optimization is crucial in numerical analysis as it often involves algorithms that seek optimal points using various techniques, including iterative methods.
Relative Error: Relative error is a measure of the uncertainty of a measurement compared to the size of the measurement itself. It expresses the error as a fraction of the actual value, providing insight into the significance of the error relative to the size of the quantity being measured. This concept is crucial in understanding how errors impact calculations in numerical analysis, particularly when dealing with different scales and precision levels.
Root-finding algorithm: A root-finding algorithm is a computational method used to find the roots (or zeros) of a real-valued function, where the function evaluates to zero. These algorithms are essential for solving equations in numerical analysis and can be categorized based on their approach, such as iterative or direct methods. They often rely on approximations and can include techniques that improve convergence to the actual root.
Secant Method: The secant method is a numerical technique used to find roots of a real-valued function by iteratively approximating the solution using secant lines. It leverages two initial guesses to produce a sequence of better approximations, each calculated from the previous two points. This method is notable for its faster convergence than the simple bisection method and requires only function evaluations rather than derivatives.
Stopping Criterion: A stopping criterion is a predefined condition that determines when an iterative numerical method should cease its computations. In the context of root-finding algorithms, such as the secant method, it helps to ensure that the process concludes once a sufficiently accurate solution has been reached, balancing computational efficiency and accuracy. Setting an appropriate stopping criterion is crucial, as it impacts both the reliability of the results and the time taken to obtain them.
Superlinear convergence: Superlinear convergence refers to a type of convergence in numerical methods where the rate at which a sequence approaches its limit is faster than linear convergence, meaning that the error decreases at a rate proportional to a power greater than one. This implies that as the iterations progress, the accuracy of the approximation improves significantly with each step, especially when close to the solution. Understanding superlinear convergence is essential for evaluating the efficiency and effectiveness of numerical algorithms, particularly those used in root-finding and optimization.
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
Back
Practice QuizGlossary
Practice QuizGlossary
Next guide