4.2 Lyapunov function construction and analysis

Lyapunov functions are key tools for analyzing stability in nonlinear systems. They're scalar functions that decrease along system trajectories, giving us insights into how the system behaves over time.

This section dives into constructing and using Lyapunov functions. We'll learn about different types, how to build them, and how to use them for stability analysis and estimating regions of attraction.

Properties of Lyapunov Functions

Definition and Conditions

Top images from around the web for Definition and Conditions

• 

  Lyapunov Stability Analysis of Certain Third Order Nonlinear Differential Equations View original

  Is this image relevant?

• 

  Find an appropriate Lyapunov function for the nonlinear system of differential equations ... View original

  Is this image relevant?

• 

  Lyapunov Stability Analysis of Certain Third Order Nonlinear Differential Equations View original

  Is this image relevant?

• 

  Find an appropriate Lyapunov function for the nonlinear system of differential equations ... View original

  Is this image relevant?

1 of 2

Top images from around the web for Definition and Conditions

• 

  Lyapunov Stability Analysis of Certain Third Order Nonlinear Differential Equations View original

  Is this image relevant?

• 

  Find an appropriate Lyapunov function for the nonlinear system of differential equations ... View original

  Is this image relevant?

• 

  Lyapunov Stability Analysis of Certain Third Order Nonlinear Differential Equations View original

  Is this image relevant?

• 

  Find an appropriate Lyapunov function for the nonlinear system of differential equations ... View original

  Is this image relevant?

1 of 2

• A Lyapunov function $V(x)$ is a positive definite scalar function defined in a region $D$ around an equilibrium point
• The function $V(x)$ must be continuously differentiable in the region $D$
• $V(x)$ must satisfy the following conditions:
  • $V(x) > 0$ for all $x \neq 0$ in the region $D$ (positive definite)
  • $V(x) = 0$ if and only if $x = 0$ (zero at the equilibrium point)
  • $V(x) \rightarrow \infty$ as $\|x\| \rightarrow \infty$ (radially unbounded)

Derivative Conditions for Stability

• The derivative of the Lyapunov function, $\dot{V}(x)$, must be negative semi-definite ($\dot{V}(x) \leq 0$) for all $x$ in the region $D$ to ensure stability
  • If $\dot{V}(x)$ is negative semi-definite, the equilibrium point is stable in the sense of Lyapunov
• If the derivative of the Lyapunov function is negative definite ($\dot{V}(x) < 0$) for all $x \neq 0$ in the region $D$, the equilibrium point is asymptotically stable
  • Asymptotic stability implies that the system trajectories converge to the equilibrium point as time approaches infinity
• If $\dot{V}(x)$ is positive definite ($\dot{V}(x) > 0$) for all $x \neq 0$ in the region $D$, the equilibrium point is unstable

Constructing Lyapunov Functions

Common Types of Lyapunov Functions

• Quadratic Lyapunov functions: $V(x) = x^{\top}Px$, where $P$ is a positive definite matrix, are commonly used for linear and nonlinear systems
  • Example: $V(x) = x_1^2 + 2x_2^2$ is a quadratic Lyapunov function for a 2-dimensional system
• Energy-based Lyapunov functions: For mechanical systems, the total energy (kinetic + potential) can often serve as a Lyapunov function candidate
  • Example: For a simple pendulum, $V(x) = \frac{1}{2}ml^2\dot{\theta}^2 + mgl(1-\cos\theta)$ is an energy-based Lyapunov function
• Sum-of-squares (SOS) method: Lyapunov functions can be constructed using SOS programming, which decomposes the function into a sum of squared polynomial terms
  • Example: $V(x) = x_1^4 + 2x_1^2x_2^2 + x_2^4$ is an SOS Lyapunov function

Methods for Constructing Lyapunov Functions

• Krasovskii's method: Given a nonlinear system $\dot{x} = f(x)$, the Lyapunov function candidate $V(x) = f^{\top}(x)f(x)$ can be used to analyze stability
• Lyapunov functions for time-varying systems: For non-autonomous systems, the Lyapunov function may explicitly depend on time, i.e., $V(x, t)$
• Lyapunov functions for systems with multiple equilibrium points: The Lyapunov function should be constructed to have a minimum at the desired equilibrium point and satisfy the required conditions in the region around it
  • Example: For a system with two stable equilibrium points, separate Lyapunov functions can be constructed for each equilibrium point

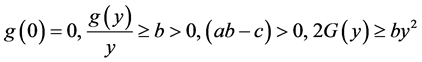
Stability Analysis with Lyapunov Functions

Calculating the Derivative of Lyapunov Functions

• The derivative of the Lyapunov function, $\dot{V}(x)$, is calculated along the system trajectories using the chain rule: $\dot{V}(x) = \nabla V(x) \cdot \dot{x}$, where $\nabla V(x)$ is the gradient of $V(x)$
  • Example: For a system $\dot{x}_1 = -x_1$ and $\dot{x}_2 = -x_2$ with $V(x) = x_1^2 + x_2^2$, $\dot{V}(x) = 2x_1\dot{x}_1 + 2x_2\dot{x}_2 = -2x_1^2 - 2x_2^2 \leq 0$

Additional Stability Analysis Tools

• LaSalle's invariance principle: If $\dot{V}(x) \leq 0$ and the set $\{x | \dot{V}(x) = 0\}$ contains no trajectories other than the equilibrium point, the equilibrium point is asymptotically stable
• Barbalat's lemma: If $V(x)$ is lower bounded, $\dot{V}(x) \leq 0$, and $\dot{V}(x)$ is uniformly continuous, then $\dot{V}(x) \rightarrow 0$ as $t \rightarrow \infty$, which can help establish asymptotic stability
  • Uniform continuity of $\dot{V}(x)$ means that for any $\varepsilon > 0$, there exists a $\delta > 0$ such that $|\dot{V}(x(t_1)) - \dot{V}(x(t_2))| < \varepsilon$ whenever $|t_1 - t_2| < \delta$

Region of Attraction Estimation

Lyapunov Stability Theorem and Sublevel Sets

• The region of attraction (ROA) is the set of all initial conditions from which the system trajectories converge to the stable equilibrium point
• Lyapunov stability theorem: If there exists a Lyapunov function $V(x)$ satisfying the stability conditions in a region $D$ around the equilibrium point, then $D$ is a subset of the ROA
• Sublevel sets of the Lyapunov function: The ROA can be estimated by finding the largest sublevel set $\{x | V(x) \leq c\}$ that is contained within the region where $\dot{V}(x) < 0$
  • Example: For a Lyapunov function $V(x) = x_1^2 + x_2^2$, the sublevel set $\{x | x_1^2 + x_2^2 \leq 1\}$ is a circle with radius 1 centered at the origin

Methods for Improving ROA Estimates

• Optimization-based methods: The ROA can be estimated by solving optimization problems that maximize the size of the sublevel set while ensuring the Lyapunov stability conditions hold
  • Example: Maximize $c$ subject to $V(x) \leq c$ and $\dot{V}(x) < 0$ for all $x$ in the region of interest
• Iterative methods: The ROA estimate can be improved by iteratively expanding the sublevel set and verifying the Lyapunov stability conditions in the enlarged region
  • Example: Start with a small sublevel set and gradually increase its size while checking the stability conditions at each iteration
• Limitations: The estimated ROA is often conservative, as it is a subset of the true ROA. The conservativeness depends on the choice of the Lyapunov function
  • A poorly chosen Lyapunov function may result in a much smaller estimated ROA compared to the true ROA