10.1 Introduction to Graphs
4 min read•august 14, 2024
Graphs are powerful tools for modeling relationships between objects. They consist of vertices (nodes) and edges connecting them, representing everything from social networks to transportation systems. Understanding graphs is key to solving complex problems in various fields.
This introduction to graphs covers their basic components, classifications, and representations. We'll explore directed and undirected graphs, different types like simple and bipartite graphs, and ways to represent them using adjacency matrices and lists.
Graphs and their components
Graph definition and components
Top images from around the web for Graph definition and components
Vertex (graph theory) - Wikipedia View original
Is this image relevant?
Eulerian path - Wikipedia View original
Is this image relevant?
Graph theory - Wikipedia View original
Is this image relevant?
Vertex (graph theory) - Wikipedia View original
Is this image relevant?
Eulerian path - Wikipedia View original
Is this image relevant?
1 of 3
Top images from around the web for Graph definition and components
Vertex (graph theory) - Wikipedia View original
Is this image relevant?
Eulerian path - Wikipedia View original
Is this image relevant?
Graph theory - Wikipedia View original
Is this image relevant?
Vertex (graph theory) - Wikipedia View original
Is this image relevant?
Eulerian path - Wikipedia View original
Is this image relevant?
1 of 3
- A graph is a mathematical structure consisting of a set of vertices (or nodes) and a set of edges that connect pairs of vertices
- Vertices represent objects or entities (people, cities, computers), while edges represent relationships or connections between the vertices (friendships, roads, network connections)
- The of a is the number of edges incident to it
- For example, in a social network graph, a person's degree would be the number of friends they have
- The degree sequence of a graph is the list of degrees of its vertices in non-increasing order
- A path in a graph is a sequence of vertices connected by edges (a route from one city to another)
- A cycle is a path that starts and ends at the same vertex (a circular route)
Graph classifications
- Graphs can be classified as:
- Null graphs: no edges
- Trivial graphs: one vertex
- Finite graphs: finite number of vertices and edges
- Infinite graphs: infinite number of vertices or edges
- Edges can be classified as:
- Loops: connecting a vertex to itself
- : more than one between the same pair of vertices
- For example, in a flight network graph, multiple edges could represent different airlines offering flights between the same cities
Directed vs Undirected Graphs
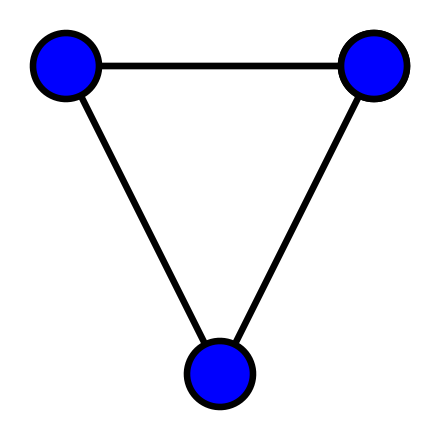
Undirected graphs
- An has edges that do not have a specific direction, meaning the relationship between vertices is symmetric or bidirectional
- For example, in a friendship graph, if person A is friends with person B, then person B is also friends with person A
- In an undirected graph, the is symmetric, meaning aij = aji for all i and j
Directed graphs
- A (or ) has edges with a specific direction, indicated by an arrow, representing an asymmetric or one-way relationship between vertices
- For example, in a web graph, a directed edge from page A to page B represents a hyperlink from A to B, but not necessarily from B to A
- In a directed graph, the of a vertex is the number of edges pointing towards it, while the is the number of edges pointing away from it
- A directed graph can have cycles, called directed cycles, where a path follows the direction of the edges and returns to the starting vertex
Types of Graphs
Simple and complete graphs
- A has no loops or multiple edges, meaning there is at most one edge between any pair of vertices
- A has an edge between every pair of vertices, denoted as Kn, where n is the number of vertices
- For example, K3 is a complete graph with 3 vertices, also known as a triangle
- The adjacency matrix of a simple graph has 0s on the main diagonal, as there are no loops
Bipartite and regular graphs
- A has its vertex set divided into two disjoint subsets, U and V, such that every edge connects a vertex in U to a vertex in V, with no edges within U or V
- For example, in a job assignment graph, U could represent employees and V could represent tasks, with edges indicating which employees are assigned to which tasks
- A , denoted as Km,n, has every vertex in U connected to every vertex in V, where |U| = m and |V| = n
- A has all vertices with the same degree, and a has all vertices of degree k
- For example, a 3-regular graph has all vertices of degree 3, meaning each vertex is connected to exactly 3 other vertices
Graph Representations
Adjacency matrices
- An adjacency matrix is a square matrix A = [aij] of size n × n, where n is the number of vertices, and aij = 1 if there is an edge from vertex i to vertex j, and 0 otherwise
- For an undirected graph, the adjacency matrix is symmetric, meaning aij = aji for all i and j
- The adjacency matrix of a simple graph has 0s on the main diagonal, as there are no loops
- Adjacency matrices are useful for dense graphs (graphs with many edges relative to the number of vertices)
Adjacency lists
- An represents a graph as an array of lists, where each element in the array corresponds to a vertex, and the list at that index contains the vertices adjacent to it
- For example, if vertex 0 is connected to vertices 1 and 2, the adjacency list would have
at index 0[1, 2] - Adjacency lists are more space-efficient than adjacency matrices for sparse graphs (graphs with few edges relative to the number of vertices)
- Adjacency lists are useful for algorithms that need to traverse the graph, as they provide direct access to the neighbors of each vertex
Key Terms to Review (31)
Adjacency list: An adjacency list is a data structure used to represent a graph, where each vertex (or node) has a list of all the vertices it is directly connected to by edges. This representation is efficient in terms of space and is particularly useful for sparse graphs, as it only stores the edges that exist. By organizing the graph in this way, it becomes easier to traverse and manipulate the graph for algorithms related to connectivity and pathfinding.
Adjacency matrix: An adjacency matrix is a square array used to represent a finite graph, where the rows and columns correspond to the vertices of the graph. Each element in the matrix indicates whether pairs of vertices are adjacent or not in the graph, with a value of 1 typically representing an edge and 0 indicating no edge. This matrix is crucial for understanding the structure of the graph and plays a significant role in analyzing paths, cycles, and connectivity within the graph.
Bipartite graph: A bipartite graph is a type of graph where the set of vertices can be divided into two distinct groups such that no two vertices within the same group are adjacent. This structure allows for the modeling of relationships between two different classes of entities, making it useful in various applications such as matching problems and network flow analysis.
Breadth-first search: Breadth-first search (BFS) is an algorithm used for traversing or searching through graph data structures. It explores all the vertices of a graph in layers, starting from a given source vertex and visiting all its immediate neighbors before moving on to the neighbors of those neighbors. This method ensures that the shortest path is found in unweighted graphs, making it a foundational concept in graph theory.
Complete bipartite graph: A complete bipartite graph is a special type of graph that consists of two disjoint sets of vertices, where every vertex from one set is connected to every vertex in the other set. This structure means there are no edges connecting vertices within the same set, making it distinct and useful for modeling relationships between two different groups. Complete bipartite graphs are denoted as K_{m,n}, where m and n represent the number of vertices in each set.
Complete Graph: A complete graph is a type of graph in which every pair of distinct vertices is connected by a unique edge. This means that in a complete graph with 'n' vertices, there are edges between every possible pair, resulting in a total of $$\frac{n(n-1)}{2}$$ edges. Complete graphs serve as fundamental structures in graph theory, facilitating the study of connectivity and relationships within various mathematical contexts.
Connectedness: Connectedness refers to a property of a graph where there is a path between every pair of vertices. This concept is important as it allows for the understanding of how different parts of a graph relate to each other. When considering connectedness, one can also explore different components of a graph, such as whether a graph is connected or disconnected, which impacts properties like the existence of spanning trees and the efficiency of traversing the graph.
Degree: In the context of graphs, the degree of a vertex is defined as the number of edges incident to that vertex. This concept helps to analyze the connectivity and structure of a graph, providing insights into its properties and behavior. The degree can indicate whether a graph is dense or sparse and plays a critical role in algorithms related to network flow and traversal.
Depth-first search: Depth-first search (DFS) is an algorithm for traversing or searching through graph data structures by exploring as far as possible along each branch before backtracking. This method allows for the exploration of nodes in a deep manner, which can be particularly useful for pathfinding and solving puzzles. DFS is commonly implemented using a stack data structure, either explicitly or via recursion, making it efficient in terms of space when navigating large graphs.
Digraph: A digraph, or directed graph, is a set of vertices connected by edges that have a direction, indicating a one-way relationship between the vertices. In digraphs, each edge is represented as an ordered pair of vertices, showing how one vertex points to another. This directional nature allows digraphs to effectively model relationships and flows in various contexts, such as computer science, social networks, and transportation systems.
Directed cycle: A directed cycle is a path in a directed graph where the starting and ending vertices are the same, and all edges are followed in the direction they point. Directed cycles are important for understanding the structure of directed graphs, as they can indicate feedback loops and relationships within data structures. Their presence or absence can also determine properties like connectivity and acyclicity, impacting algorithms used for graph traversal and optimization.
Directed graph: A directed graph, also known as a digraph, is a set of vertices connected by edges that have a specific direction. Each edge in a directed graph points from one vertex to another, indicating a one-way relationship, unlike undirected graphs where the connection is bidirectional. This directional aspect allows for various applications, such as representing relationships in social networks, workflows in project management, or pathways in navigation systems.
Edge: An edge is a fundamental component of a graph that connects two vertices, representing a relationship or link between them. Edges can be directed or undirected, indicating whether the relationship has a specific direction or is bidirectional. Understanding edges is crucial because they help to illustrate various types of relationships and structures within mathematical and real-world contexts, such as networks, trees, and more complex systems.
Euler's Theorem: Euler's Theorem states that for any two coprime integers $a$ and $n$, it holds that $a^{\phi(n)} \equiv 1 \pmod{n}$, where $\phi(n)$ is Euler's totient function, which counts the positive integers up to $n$ that are relatively prime to $n$. This theorem is fundamental in number theory and has applications in various areas such as cryptography and combinatorics.
Finite graph: A finite graph is a type of graph that contains a finite number of vertices and edges. This means that both the nodes (or points) and the connections between them are countable and limited. Finite graphs are often used to model real-world problems in various fields such as computer science, biology, and social sciences, where the relationships or interactions can be represented in a manageable way.
In-degree: In a directed graph, the in-degree of a vertex is the number of edges directed into that vertex. This concept is crucial for understanding the flow of information and relationships within the graph, as it indicates how many connections or influences are coming towards a specific node. The in-degree helps in analyzing network structures, as it can reflect the importance or popularity of nodes within various applications like social networks, web pages, and more.
Infinite graph: An infinite graph is a type of graph that contains an infinite number of vertices and edges, meaning it does not have a finite limit to its size. These graphs can represent complex structures, like networks or relationships, that extend indefinitely. Infinite graphs can be used in various mathematical contexts, including topology, set theory, and combinatorics, showcasing unique properties that differ from finite graphs.
Isomorphic Graphs: Isomorphic graphs are two or more graphs that can be transformed into each other by relabeling their vertices while preserving the structure of the connections between them. This means that there is a one-to-one correspondence between their vertex sets and edge sets, highlighting the idea that the graphs share the same shape or form despite potentially having different appearances or labels.
K-regular graph: A k-regular graph is a type of graph where each vertex has the same degree k, meaning that every vertex is connected to exactly k edges. This property ensures uniformity in the connections among the vertices, making it easier to analyze certain characteristics such as connectivity and the overall structure of the graph. These graphs can represent various real-world systems, including social networks and communication systems.
Loop: In graph theory, a loop is an edge that connects a vertex to itself. This means that the edge starts and ends at the same vertex, effectively creating a cycle of length one. Loops are interesting because they allow for unique behaviors in the graph, affecting the degree of vertices and the overall structure.
Minimum spanning tree: A minimum spanning tree is a subset of the edges of a connected, undirected graph that connects all the vertices together without any cycles and with the minimum possible total edge weight. This concept is essential in optimizing network design, ensuring efficient connection between nodes while minimizing costs associated with the connections.
Multiple edges: Multiple edges are two or more edges that connect the same pair of vertices in a graph. This feature allows for more complex relationships between nodes, enhancing the graph's representation of real-world connections. While many graphs consider only a single edge between two vertices, allowing multiple edges can provide a richer understanding of interactions and dependencies.
Null graph: A null graph is a graph that contains no vertices and, consequently, no edges. This means it has an empty set of points and is often considered the simplest form of a graph. Null graphs serve as a fundamental concept in graph theory, providing a base case for various definitions and theorems related to graphs.
Out-degree: Out-degree is a concept in graph theory that refers to the number of edges leaving a vertex in a directed graph. It represents how many connections or relationships a particular node has with other nodes when considering directionality. The out-degree provides insight into the importance and influence of a vertex within the structure of the graph, as it reflects how much that vertex contributes to outgoing relationships.
Regular Graph: A regular graph is a type of graph in which every vertex has the same number of edges, meaning each vertex has the same degree. This uniformity in connection creates a balanced structure, which can lead to interesting properties and behaviors in graph theory. Regular graphs can be classified into different types based on their degree, such as k-regular graphs, where every vertex has degree k.
Shortest path: The shortest path refers to the minimum distance or minimum weight route between two vertices in a graph. This concept is vital when analyzing graphs, as it helps in finding efficient routes, whether for transportation, networking, or resource allocation. Finding the shortest path not only optimizes travel time or costs but also connects various points effectively, emphasizing the importance of paths and cycles within graphs.
Simple graph: A simple graph is an undirected graph that does not contain multiple edges between any pair of vertices and has no loops. This means that each edge connects two distinct vertices and there is at most one edge connecting any two vertices. Simple graphs are fundamental in graph theory, as they provide a clear and structured way to represent relationships between objects without complexity.
Subgraph: A subgraph is a portion of a graph that consists of a selection of its vertices and the edges that connect them. This concept allows for the analysis of smaller sections of larger graphs, making it easier to study specific properties and relationships within the overall structure. Subgraphs can be used in various contexts, such as finding particular paths or understanding components of a network.
Trivial graph: A trivial graph is a graph that contains only one vertex and no edges. This simple structure forms the most basic type of graph, providing a foundation for understanding more complex graph concepts. In terms of properties, it serves as an essential example when discussing graph connectivity and isolation since it lacks any relationships or connections that are typically present in larger graphs.
Undirected graph: An undirected graph is a collection of vertices connected by edges where the edges have no direction. This means that the connection between any two vertices is bidirectional, allowing movement from one vertex to another without a specified starting or ending point. This characteristic enables undirected graphs to represent relationships where the direction does not matter, such as friendships in social networks or connections in computer networks.
Vertex: A vertex is a fundamental component in graph theory, representing a point where edges meet or intersect. It serves as a node in a graph, helping to define the structure and relationships within the graph. Understanding vertices is crucial for analyzing properties such as connectivity, paths, and cycles, which are essential for various applications in mathematics, computer science, and operations research.