Glossary

8.1 Optimality conditions for unconstrained problems

3 min read•july 30, 2024

Unconstrained optimization is all about finding the best solution without any limits. We'll look at how to spot optimal points using gradients and Hessian matrices, which tell us about a function's slope and curvature.

We'll also explore the difference between local and global optima, and how convexity affects our search. Understanding these concepts is key to solving real-world problems where we want to maximize or minimize something.

Optimality Conditions for Unconstrained Optimization

Gradient and Hessian in Optimality Conditions

Top images from around the web for Gradient and Hessian in Optimality Conditions

  • Hessian transfer for multilevel and adaptive shape optimization | International Journal for ... View original

    Is this image relevant?

  • The Hessian-vector product H v E (δv ) is computed from the incremental equations associated to ... View original

    Is this image relevant?

  • Hessian transfer for multilevel and adaptive shape optimization | International Journal for ... View original

    Is this image relevant?

1 of 3

Top images from around the web for Gradient and Hessian in Optimality Conditions

  • Hessian transfer for multilevel and adaptive shape optimization | International Journal for ... View original

    Is this image relevant?

  • The Hessian-vector product H v E (δv ) is computed from the incremental equations associated to ... View original

    Is this image relevant?

  • Hessian transfer for multilevel and adaptive shape optimization | International Journal for ... View original

    Is this image relevant?

1 of 3
  • (FONC) for local optimum requires of objective function to equal zero at optimal point
  • Gradient vector ∇f(x) contains first-order partial derivatives of objective function f(x) with respect to each decision variable
  • (SONC) involves of objective function
    • Must be for
    • Must be for local maximum
  • Hessian matrix H(x) contains second-order partial derivatives of f(x)
  • (SOSC) for local minimum requires matrix at

Global Optimality and Coercivity

  • Global optimality conditions depend on convexity or concavity of objective function over entire feasible region
  • For , stationary point becomes if function convex and global maximum if function concave
  • concept crucial for establishing existence of global optima in unbounded domains
    • Occurs when objective function approaches infinity as decision variables approach infinity
  • Global optimality more challenging to determine in non-convex problems

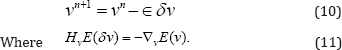
First- and Second-Order Optimality Conditions

Identifying and Classifying Stationary Points

  • Stationary point identified when gradient vector equals zero (∇f(x) = 0)
  • Hessian matrix used to classify stationary points
    • Positive definite Hessian indicates local minimum
    • indicates local maximum
    • Indefinite Hessian indicates (neither local minimum nor maximum)
  • of Hessian matrix at stationary point determine its definiteness
    • All positive eigenvalues indicate positive definiteness (local minimum)
    • All negative eigenvalues indicate negative definiteness (local maximum)
    • Mixed positive and negative eigenvalues indicate indefiniteness (saddle point)
  • Singular Hessian (zero eigenvalue) may require higher-order derivatives to determine nature of stationary point

Examples of Optimality Conditions

  • Quadratic function: f(x)=x2+2y2f(x) = x^2 + 2y^2
    • Gradient: ∇f(x,y) = (2x, 4y)
    • Hessian: H=[2004]H = \begin{bmatrix} 2 & 0 \\ 0 & 4 \end{bmatrix}
    • Stationary point at (0,0), positive definite Hessian indicates local minimum
  • Saddle function: f(x,y)=x2−y2f(x,y) = x^2 - y^2
    • Gradient: ∇f(x,y) = (2x, -2y)
    • Hessian: H=[200−2]H = \begin{bmatrix} 2 & 0 \\ 0 & -2 \end{bmatrix}
    • Stationary point at (0,0), indefinite Hessian indicates saddle point

Convex vs Non-Convex Optimization Problems

Properties of Convex Optimization

  • Function f(x) convex if line segment between any two points on its graph lies above or on graph
  • Second-order condition for convexity requires positive semidefinite Hessian matrix for all x in domain
  • Convex optimization problems have simplified optimal solution search
    • Any local minimum also global minimum
  • Set of optimal solutions for convex problem forms convex set
  • Convex problems satisfy Karush-Kuhn-Tucker (KKT) conditions as necessary and sufficient conditions for optimality

Challenges in Non-Convex Optimization

  • Non-convex optimization problems may have multiple local optima
    • Challenging to determine global optimum
  • Non-convex problems may have disconnected sets of optimal solutions
  • necessary but not sufficient for global optimality in non-convex problems
    • Requires additional global optimization techniques (genetic algorithms, simulated annealing)
  • Examples of non-convex functions
    • f(x)=x4−2x2+1f(x) = x^4 - 2x^2 + 1 (multiple local minima)
    • f(x,y)=x2+y2+sin⁡(xy)f(x,y) = x^2 + y^2 + \sin(xy) (oscillating surface with multiple local optima)

Key Terms to Review (19)

Coercivity: Coercivity refers to a property of a function that ensures its lower boundedness, meaning that the function does not approach negative infinity as its argument goes to infinity. This characteristic is crucial for guaranteeing that optimization problems have solutions, particularly in the context of unconstrained problems where one seeks to minimize a function over its entire domain. In simpler terms, coercivity helps us make sure that as we move away from the center of our problem space, the function values keep growing, preventing them from dropping infinitely low.
Concave Function: A concave function is a type of mathematical function where, for any two points on the graph, the line segment connecting these points lies below or on the graph itself. This property implies that a concave function has a downward-sloping shape, which is crucial in optimization as it indicates that any local maximum is also a global maximum. Understanding concave functions helps identify optimal solutions in various mathematical and economic models.
Convex function: A convex function is a type of mathematical function where a line segment joining any two points on the graph of the function lies above or on the graph itself. This property indicates that local minima are also global minima, making convex functions especially important in optimization problems, particularly when determining optimality conditions, unconstrained problems, and methods like Newton's method. Understanding convex functions also helps with duality in semidefinite programming and the characteristics of convex sets.
Eigenvalues: Eigenvalues are special numbers associated with a square matrix that provide insights into the properties of linear transformations represented by that matrix. Specifically, eigenvalues indicate how much a corresponding eigenvector is stretched or compressed during that transformation. This concept is crucial when determining the optimality conditions for unconstrained problems, as they help analyze the curvature of functions and identify local minima or maxima.
First-order necessary condition: The first-order necessary condition is a mathematical criterion used to determine whether a point is a local extremum (minimum or maximum) of a function. Specifically, it states that for a differentiable function, the gradient at that point must be zero, meaning there is no slope at that location, which indicates a potential extremum.
Global minimum: A global minimum refers to the lowest point in a function's entire domain, representing the smallest value that the function can attain. Identifying a global minimum is crucial for optimization problems, as it determines the most efficient outcome among all possible solutions. This concept is intimately linked with optimality conditions, the use of Lagrange multipliers in constrained scenarios, and the characteristics of convex functions, which often simplify the search for these minima.
Gradient: The gradient is a vector that contains the partial derivatives of a function, pointing in the direction of the steepest ascent of that function. It helps in identifying optimal solutions by showing how a small change in input can affect the output, which is crucial for optimization problems, especially in understanding where local maxima and minima occur.
Hessian Matrix: The Hessian matrix is a square matrix of second-order partial derivatives of a scalar-valued function, providing important information about the curvature of the function's graph. It is critical in optimization as it helps determine the nature of critical points, indicating whether they are local minima, local maxima, or saddle points based on its eigenvalues.
KKT Conditions: KKT conditions, or Karush-Kuhn-Tucker conditions, are a set of mathematical criteria used to determine the optimality of a solution in constrained optimization problems. These conditions extend the concept of optimality by incorporating constraints into the analysis, allowing for the identification of optimal solutions under both equality and inequality constraints. They form a crucial bridge between unconstrained and constrained optimization methods, enhancing the understanding of how solutions can be efficiently found in various mathematical contexts.
Local minimum: A local minimum is a point in a function where the function value is lower than the values of the surrounding points within a certain neighborhood. This concept is crucial in optimization because it helps identify potential solutions to problems, although a local minimum does not guarantee that it's the lowest point overall, known as the global minimum. Understanding local minima is essential for finding optimal solutions in various mathematical contexts, particularly when assessing the behavior of functions and analyzing convexity.
Negative Definite Hessian: A negative definite Hessian is a matrix that indicates that a function is locally concave down at a point, meaning that the second derivative test shows the presence of a local maximum. In optimization problems, this characteristic is essential for identifying critical points where the function achieves maximum values. The negative definiteness implies that all eigenvalues of the Hessian matrix are negative, confirming that the function curves downward in all directions around that point.
Negative semidefinite: A matrix is considered negative semidefinite if all its eigenvalues are less than or equal to zero, which indicates that it does not have any positive curvature. This property is crucial when determining the nature of critical points in optimization problems, particularly for identifying whether a point is a maximum. In the context of optimization, negative semidefinite matrices play an important role in characterizing the behavior of functions around critical points.
Positive Definite Hessian: A positive definite Hessian is a square matrix of second-order partial derivatives of a function that indicates the function is locally convex at a given point. When the Hessian is positive definite, it means all its eigenvalues are positive, which confirms that the critical point is a local minimum. This property is crucial in optimization as it helps to identify whether a solution is optimal.
Positive Semidefinite: A matrix is considered positive semidefinite if it is symmetric and all its eigenvalues are non-negative. This concept is crucial in various optimization problems, particularly when determining the nature of critical points, and also plays a vital role in the formulation of dual problems in semidefinite programming. Understanding positive semidefinite matrices helps ensure that certain optimization conditions are satisfied and provides insights into the stability of solutions.
Saddle Point: A saddle point is a critical point on a surface that serves as a minimum in one direction and a maximum in another. This unique characteristic allows it to be a candidate for optimization in unconstrained problems, where it indicates that the function does not achieve a local optimum but rather an inflection point of sorts. Identifying saddle points is crucial as they can impact the convergence of optimization algorithms.
Second-order necessary condition: The second-order necessary condition is a criterion used in optimization to determine whether a candidate point is a local minimum. It states that for a function to have a local minimum at a point, not only must the first derivative (gradient) equal zero at that point, but the second derivative (Hessian) must also be positive semi-definite. This concept is essential for distinguishing between local minima, maxima, and saddle points in optimization problems.
Second-order sufficient condition: The second-order sufficient condition is a criterion used in optimization to determine whether a candidate point is a local minimum of a function. Specifically, for a function to have a local minimum at a point, the first derivative must be zero (indicating a critical point), and the second derivative must be positive at that point, confirming that the curvature is upward. This condition ensures that the function behaves well around the critical point, thus establishing local optimality.
Stationary point: A stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the function's value at that point. These points are critical for finding local maxima, minima, or saddle points in optimization problems, as they represent candidates for optimal solutions in unconstrained scenarios.
Twice Continuously Differentiable Function: A twice continuously differentiable function is a real-valued function that has continuous first and second derivatives. This property ensures that not only does the function itself change smoothly, but also the rate of change (first derivative) and the rate of acceleration (second derivative) are both smooth. This characteristic is essential when analyzing optimality conditions for functions, as it provides the necessary mathematical structure to apply critical point tests and guarantees the existence of certain optimization properties.
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
Back
Practice QuizGlossary
Practice QuizGlossary
Next guide