5.2 Routh-Hurwitz Stability Criterion

The Routh-Hurwitz Stability Criterion is a powerful tool for checking system stability without solving complex equations. It uses a simple array of coefficients to determine if a system is stable, unstable, or on the edge.

This method is super helpful for higher-order systems where finding roots is a pain. By looking at sign changes in the array, you can quickly figure out if a system will behave or go haywire.

Routh-Hurwitz Stability Criterion

Overview of the Routh-Hurwitz Stability Criterion

Top images from around the web for Overview of the Routh-Hurwitz Stability Criterion

• 

  A Modified Stability Analysis of Two-Dimensional Linear Time Invariant Discrete Systems within ... View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

• 

  A Modified Stability Analysis of Two-Dimensional Linear Time Invariant Discrete Systems within ... View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

1 of 3

Top images from around the web for Overview of the Routh-Hurwitz Stability Criterion

• 

  A Modified Stability Analysis of Two-Dimensional Linear Time Invariant Discrete Systems within ... View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

• 

  A Modified Stability Analysis of Two-Dimensional Linear Time Invariant Discrete Systems within ... View original

  Is this image relevant?

• 

  HurwitzMatrix | Wolfram Function Repository View original

  Is this image relevant?

1 of 3

• The Routh-Hurwitz stability criterion is a mathematical test used to determine the stability of a linear time-invariant (LTI) system without explicitly solving for the roots of the characteristic equation
• The criterion is based on the coefficients of the characteristic equation and provides a necessary and sufficient condition for the stability of the system
• A system is considered stable if all the roots of its characteristic equation have negative real parts, meaning they lie in the left half of the complex plane (s-plane)
• The criterion is particularly useful for analyzing the stability of higher-order systems, where finding the roots of the characteristic equation can be challenging or time-consuming (4th order or higher)

Historical Background and Significance

• The Routh-Hurwitz criterion is named after Edward John Routh and Adolf Hurwitz, who independently developed the method in the late 19th century
• The criterion has become a fundamental tool in control systems engineering and is widely used to assess the stability of various systems, such as electrical circuits, mechanical systems, and feedback control systems
• By determining the stability of a system without explicitly solving for the roots, the Routh-Hurwitz criterion saves time and effort in the analysis process
• The criterion also provides insights into the system's behavior and can help in the design of stable control systems

Constructing the Routh Array

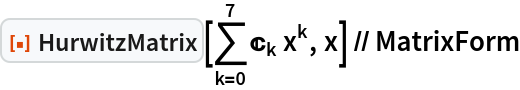
Arranging the Coefficients of the Characteristic Equation

• The Routh array is a tabular arrangement of the coefficients of the characteristic equation, which is used to determine the number of roots with positive real parts
• To construct the Routh array, arrange the coefficients of the characteristic equation in descending order of the power of s
• The first two rows of the array are formed directly from the coefficients of the characteristic equation, with the even-indexed coefficients in the first row and the odd-indexed coefficients in the second row
• For example, given a characteristic equation: $a_4s^4 + a_3s^3 + a_2s^2 + a_1s + a_0 = 0$, the first two rows of the Routh array would be: | $s^4$ | $a_4$ | $a_2$ | $a_0$ | | $s^3$ | $a_3$ | $a_1$ | 0 |

Generating Subsequent Rows Using the Recursive Formula

• The subsequent rows of the array are generated using a recursive formula that involves the coefficients from the two previous rows
• The formula for the elements in the ith row and jth column is: $(a[i-1][1] * a[i-2][j+1] - a[i-1][j+1] * a[i-2][1]) / a[i-1][1]$, where $a[i][j]$ represents the element in the ith row and jth column
• The process continues until a row with all zeros is encountered or the last row is completed
• If a zero is encountered in the first column during the construction of the Routh array, it is replaced by a small positive parameter $ε$, and the limit of the Routh array is evaluated as $ε$ approaches zero

System Stability Analysis

Applying the Routh-Hurwitz Criterion

• The Routh-Hurwitz criterion states that the number of roots of the characteristic equation with positive real parts is equal to the number of sign changes in the first column of the Routh array
• For a system to be stable, all the elements in the first column of the Routh array must have the same sign (either all positive or all negative)
• If any element in the first column is zero, it indicates the presence of roots on the imaginary axis, and further investigation is required to determine the stability of the system
• If there are no sign changes in the first column and no elements are zero, the system is stable
• If there are one or more sign changes in the first column, the system is unstable, and the number of sign changes equals the number of roots with positive real parts

Handling Special Cases and Marginal Stability

• When a zero element is encountered in the first column during the construction of the Routh array, it is replaced by a small positive parameter $ε$, and the limit of the Routh array is evaluated as $ε$ approaches zero
• If the zero element persists in the limit, it indicates the presence of roots on the imaginary axis, and the system is considered marginally stable
• Marginal stability implies that the system's response to disturbances neither grows nor decays over time, and the system oscillates with a constant amplitude
• In cases of marginal stability, additional analysis, such as examining the system's time response or frequency response, may be necessary to fully understand the system's behavior

Routh-Hurwitz for Higher-Order Systems

Analyzing Stability of Higher-Order Systems

• The Routh-Hurwitz criterion is particularly useful for analyzing the stability of systems described by higher-order characteristic equations (e.g., 3rd order or higher)
• To apply the criterion, first write the characteristic equation of the system in descending order of the power of s
• Construct the Routh array using the coefficients of the characteristic equation, following the procedure described in the previous sections
• Examine the first column of the Routh array for sign changes and zero elements to determine the stability of the system
• If necessary, investigate any zero elements in the first column by replacing them with a small positive parameter $ε$ and evaluating the limit of the Routh array as $ε$ approaches zero

Applications in Various Fields

• The Routh-Hurwitz criterion can be used to analyze the stability of systems in various fields, such as control systems, electrical circuits, and mechanical systems, without explicitly solving for the roots of the characteristic equation
• In control systems engineering, the criterion is used to design stable controllers and analyze the stability of closed-loop systems (PID controllers, lead-lag compensators)
• In electrical engineering, the Routh-Hurwitz criterion is applied to assess the stability of electrical circuits and power systems (RLC circuits, power grid stability)
• Mechanical engineers use the criterion to study the stability of mechanical systems, such as vibrating structures, and to design stable control systems for machines and robots (active suspension systems, robotic manipulators)