
Volume of a Sphere, Cylinder, and Cone
5 min read•december 13, 2021
William
William
Formulas and Practice to Solve for the Volume a Sphere, Cylinder, and Cone
Several similarities and differences exist between these three-dimensional figures, including having curvy (rather than flat) sides! However, each has unique features that differentiate it from another 3D object. Let’s get started!
Want the Formulas Now?
The table below displayed the volume equations for a sphere, cylinder, and cone. The information following this chart provides more in-depth information that will help you identify and distinguish one 3D object from another and practice using these formulas with a few equations.
Sphere | V = 4/3𝞹r^3 |
Cylinder | V = 𝞹r^2h |
Cone | V = ⅓𝞹r^2h |
Features of a Sphere
A sphere is a 3D object where the distance from the center point is the same. In other words, the sphere’s radius (distance from the center to the sphere’s surface) is the same in any direction in the 3D space. A sphere is entirely symmetrical, rounded, and lacks flat sides and edges.

Image courtesy of Wikipedia
Final Equation
V = 4/3𝞹r^3, where V is the final volume and r3 represents the distance from the sphere's center to its surface, with the superscript confirming the sphere's 3D features. Understanding the concept behind the meaning of the 4/3 and 𝞹 would require the knowledge of higher-level mathematics. Regardless, it essentially encompasses a cylindrical element that contributes to the final volume of a sphere.
Features of a Cylinder
A cylinder is a prism with two circular bases and parallel sides that connect these two bases. These parallel sides that join the two flat circular ends form a tube-like shape. This object has two faces (the two circular bases) and two rims (the parallel sides that meet the rims of the two bases). Its overall shape is similar to that of a tin can.
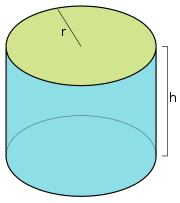
Image courtesy of Wikipedia
Final Equation
V = 𝞹r^2h, where V is the final volume of the cylinder. Notice how rather than r^3 in the spherical equation, the cylindrical equation uses r^2? Since h of this equation compensates for the cylinder's height, 𝞹r2 represents the area of the circle (2D), which is why the subscript for r is 2. The height of the cylinder multiplied by the area of the flat circle produces the final volume.
Features of a Cone
A cone includes a circular base and an apex, otherwise known as the highest point of this object. The apex sits above the base's center, and there is a surface area extending from the apex to the base's border. This 3D object has one face, the base, and one edge, the rim of the circular base.
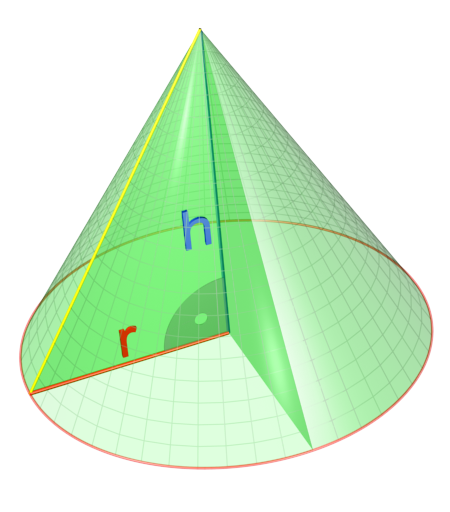
Image courtesy of Wikipedia
Final Equation
V = ⅓𝞹r^2h, where V is the final volume of 𝞹r^2, the base of the cone, and h is the height of the cone.
Explaining 𝞹r2
Did you notice a relationship between the cylinder and cone’s features? If you noticed that one part of the equation is 𝞹r^2, great work! This is the same formula as that of a 2D circle's area, and multiplying this with the height produces a final volume. This is the same formula as that of a 2D circle's area, and multiplying this with the height produces a final volume.
Similarly, the volume of a rectangular prism is lwh, where lw forms the prism's base as length and width, and multiplying height h to this provides the volume.

GIF courtesy of GIPHY
Solving Problems with Spheres, Cylinders, and Cones
If you're taking the SAT, you will likely encounter a couple of problems requiring you to solve for a missing value with limited information about that specific object. Using the equations provided above, try solving these three problems! You can find the answers and explanations at the bottom of this page.
Problem 1 - Easy
The distance between the center and any point on the boundary of the sphere is 3 centimeters. Calculate the volume of the sphere.
Problem 2 - Medium
Juan recently purchased canned corn from the local grocery store. In preparation for his upcoming test, he decided he wanted to try and find the volume of the can. He found that the height of the can was 4.5 inches tall and 3 inches wide. What is the volume of the can in terms of pi?
(Hint: What is the shape of a can?)
Problem 3 - Difficult
Matilda passes through construction work on the highway and wants to know the diameter of one of the traffic cones. What is the diameter of the cone if the volume is 180 in3 and the cone is 24 inches tall?
Answers
Problem 1
“The distance between the center and any point on the boundary of the sphere is 3 centimeters. Calculate the volume of the sphere.”
Since we know that the sphere's radius is 3 centimeters, we can plug that into our volume equation for a sphere to find the volume!
Problem 2
“Juan recently purchased canned corn from the local grocery store. In preparation for his upcoming test, he decided he wanted to try and find the volume of the can. He found that the height of the can was 4.5 inches tall and 3 inches wide. What is the volume of the can in terms of pi?”
We know that the height of the can is 4.5 inches, and the diameter is 3 inches. With this in mind, let’s first calculate the area of the base using the diameter, then plug that into the equation for the cylinder. Recall that A = 𝝅r^2, and the diameter is equal to 2r. To find r, let’s divide the diameter by two: r = 3in/2 = 1.5in. Now that we have all the values we need, let’s plug it into the equation for a cylinder!
Problem 3
“Matilda passes through construction work on the highway and wants to know the diameter of one of the traffic cones. What is the diameter of the cone if the volume is 180in3 and the cone is 24 inches tall?”
Let’s start by plugging in the values and isolating r!
Multiply both sides by 3:
Divide both sides by 4.92𝞹:
Find the square root of both sides:
Notice that we’re not done yet because the problem wants us to find the diameter! Recall that r is from the center to one end of the boundary. We can use 2r to find the entire length across the base.
What to Take Away
Spheres, cylinders, and cones are incredibly important for not only solving SAT problems, but also for applicable problems in real life! When calculating the volume of a circular 3D object, the width and length use A = 𝞹r2, which is the area of a 2D circle. Finding the relationship between 2D and 3D figures is always useful when approaching problems. Good luck on your studies! 👌
Sources
Volume of a Sphere, Cylinder, and Cone
5 min read•december 13, 2021
William
William
Formulas and Practice to Solve for the Volume a Sphere, Cylinder, and Cone
Several similarities and differences exist between these three-dimensional figures, including having curvy (rather than flat) sides! However, each has unique features that differentiate it from another 3D object. Let’s get started!
Want the Formulas Now?
The table below displayed the volume equations for a sphere, cylinder, and cone. The information following this chart provides more in-depth information that will help you identify and distinguish one 3D object from another and practice using these formulas with a few equations.
Sphere | V = 4/3𝞹r^3 |
Cylinder | V = 𝞹r^2h |
Cone | V = ⅓𝞹r^2h |
Features of a Sphere
A sphere is a 3D object where the distance from the center point is the same. In other words, the sphere’s radius (distance from the center to the sphere’s surface) is the same in any direction in the 3D space. A sphere is entirely symmetrical, rounded, and lacks flat sides and edges.

Image courtesy of Wikipedia
Final Equation
V = 4/3𝞹r^3, where V is the final volume and r3 represents the distance from the sphere's center to its surface, with the superscript confirming the sphere's 3D features. Understanding the concept behind the meaning of the 4/3 and 𝞹 would require the knowledge of higher-level mathematics. Regardless, it essentially encompasses a cylindrical element that contributes to the final volume of a sphere.
Features of a Cylinder
A cylinder is a prism with two circular bases and parallel sides that connect these two bases. These parallel sides that join the two flat circular ends form a tube-like shape. This object has two faces (the two circular bases) and two rims (the parallel sides that meet the rims of the two bases). Its overall shape is similar to that of a tin can.

Image courtesy of Wikipedia
Final Equation
V = 𝞹r^2h, where V is the final volume of the cylinder. Notice how rather than r^3 in the spherical equation, the cylindrical equation uses r^2? Since h of this equation compensates for the cylinder's height, 𝞹r2 represents the area of the circle (2D), which is why the subscript for r is 2. The height of the cylinder multiplied by the area of the flat circle produces the final volume.
Features of a Cone
A cone includes a circular base and an apex, otherwise known as the highest point of this object. The apex sits above the base's center, and there is a surface area extending from the apex to the base's border. This 3D object has one face, the base, and one edge, the rim of the circular base.

Image courtesy of Wikipedia
Final Equation
V = ⅓𝞹r^2h, where V is the final volume of 𝞹r^2, the base of the cone, and h is the height of the cone.
Explaining 𝞹r2
Did you notice a relationship between the cylinder and cone’s features? If you noticed that one part of the equation is 𝞹r^2, great work! This is the same formula as that of a 2D circle's area, and multiplying this with the height produces a final volume. This is the same formula as that of a 2D circle's area, and multiplying this with the height produces a final volume.
Similarly, the volume of a rectangular prism is lwh, where lw forms the prism's base as length and width, and multiplying height h to this provides the volume.

GIF courtesy of GIPHY
Solving Problems with Spheres, Cylinders, and Cones
If you're taking the SAT, you will likely encounter a couple of problems requiring you to solve for a missing value with limited information about that specific object. Using the equations provided above, try solving these three problems! You can find the answers and explanations at the bottom of this page.
Problem 1 - Easy
The distance between the center and any point on the boundary of the sphere is 3 centimeters. Calculate the volume of the sphere.
Problem 2 - Medium
Juan recently purchased canned corn from the local grocery store. In preparation for his upcoming test, he decided he wanted to try and find the volume of the can. He found that the height of the can was 4.5 inches tall and 3 inches wide. What is the volume of the can in terms of pi?
(Hint: What is the shape of a can?)
Problem 3 - Difficult
Matilda passes through construction work on the highway and wants to know the diameter of one of the traffic cones. What is the diameter of the cone if the volume is 180 in3 and the cone is 24 inches tall?
Answers
Problem 1
“The distance between the center and any point on the boundary of the sphere is 3 centimeters. Calculate the volume of the sphere.”
Since we know that the sphere's radius is 3 centimeters, we can plug that into our volume equation for a sphere to find the volume!
Problem 2
“Juan recently purchased canned corn from the local grocery store. In preparation for his upcoming test, he decided he wanted to try and find the volume of the can. He found that the height of the can was 4.5 inches tall and 3 inches wide. What is the volume of the can in terms of pi?”
We know that the height of the can is 4.5 inches, and the diameter is 3 inches. With this in mind, let’s first calculate the area of the base using the diameter, then plug that into the equation for the cylinder. Recall that A = 𝝅r^2, and the diameter is equal to 2r. To find r, let’s divide the diameter by two: r = 3in/2 = 1.5in. Now that we have all the values we need, let’s plug it into the equation for a cylinder!
Problem 3
“Matilda passes through construction work on the highway and wants to know the diameter of one of the traffic cones. What is the diameter of the cone if the volume is 180in3 and the cone is 24 inches tall?”
Let’s start by plugging in the values and isolating r!
Multiply both sides by 3:
Divide both sides by 4.92𝞹:
Find the square root of both sides:
Notice that we’re not done yet because the problem wants us to find the diameter! Recall that r is from the center to one end of the boundary. We can use 2r to find the entire length across the base.
What to Take Away
Spheres, cylinders, and cones are incredibly important for not only solving SAT problems, but also for applicable problems in real life! When calculating the volume of a circular 3D object, the width and length use A = 𝞹r2, which is the area of a 2D circle. Finding the relationship between 2D and 3D figures is always useful when approaching problems. Good luck on your studies! 👌
Sources

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.