
Distance Formula and Distance Between Two Points
3 min read•november 23, 2021
Jaaziel Sandoval
Jaaziel Sandoval
Using the Distance Formula and Finding Distance Between Two Points
Introduction to the Distance Formula
Graphs can be a huge pain, especially if you don’t know where to start. The good news is that formulas exist to make life easier! A formula that comes in handy a lot is the distance formula. This formula is derived from the Pythagorean Theorem and is used to find the distance between two points on a graph.
The Formula
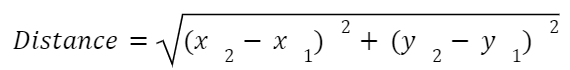
Let’s unpack this formula. x1 , y1refers to the first point you choose and x2 , y2 refers to the second point you choose. Note: It doesn’t matter which point you pick first or second as long as you make sure that you plug them in correctly in the formula! If you’re a bit confused right now, you’ll understand better after doing some practice.
Practice
Find the distance between the two points shown on the graph.

Solution
Choose the red point as x1 , y 1 and the blue point for x2 , y 2. Then, simply plug the coordinates into the distance formula:
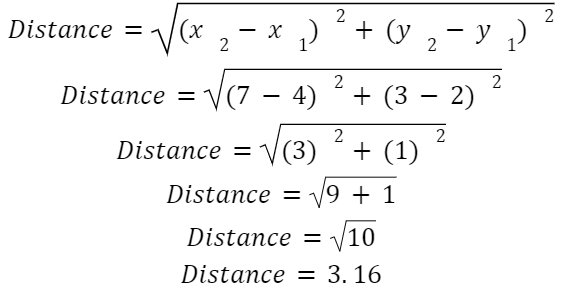
It’s that easy. Remember how it was mentioned that it didn’t matter which point you chose for x1 , y 1 and x2 , y 2? Let’s see why. Choose the blue point as x1 , y 1 and the red point for x2 , y 2 and plug in the coordinates:
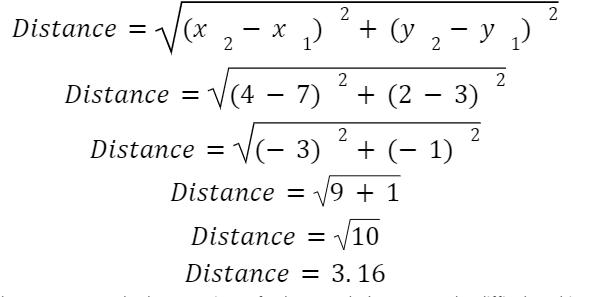
We got the same answer both ways! Piece of cake! Now, let’s ramp up the difficulty a bit. Find the distance between the two points shown on the graph.
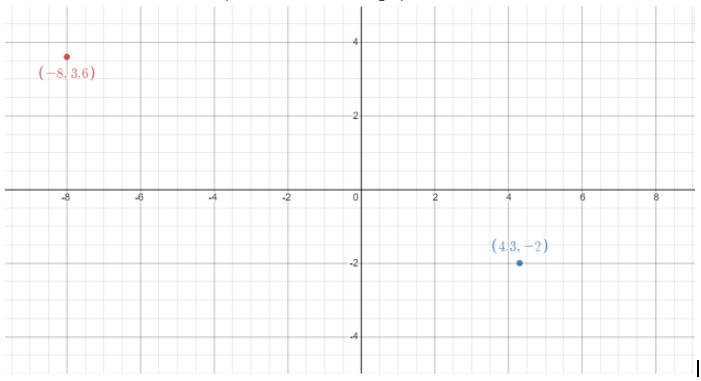
Solution
Choose the red point as x1 , y 1 and the blue point for x2 , y 2. Then, simply plug in the coordinates:
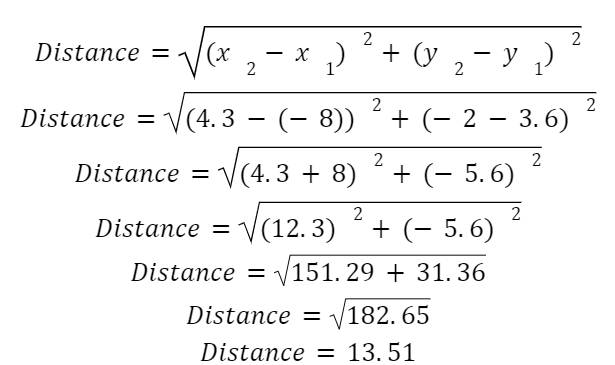
Bam! Easy! Ok, now that we’ve mastered this, let’s spice it up a bit. What happens if you’re given the distance and all of the coordinates except for one. Not to worry, we can just reverse engineer this and get it done. Let’s practice with a word problem instead of a graph this time.
Find the missing point from a line with a distance of 5 and coordinates of (10,7) and (r,3).
Solution
To solve this just plug all the given components, including the unknown variable r, into the formula:
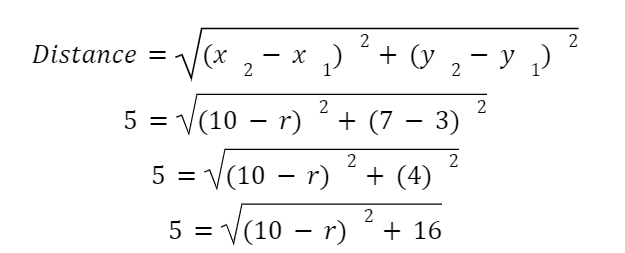
PAUSE! We’ve simplified it as much as we could, now what do we do? We will now expand (10-r)2. If you need help with this or with using the quadratic formula, check out this article from Fiveable. (10-r)2 can be expanded to r2 - 20r + 100, which we can now plug into the formula:
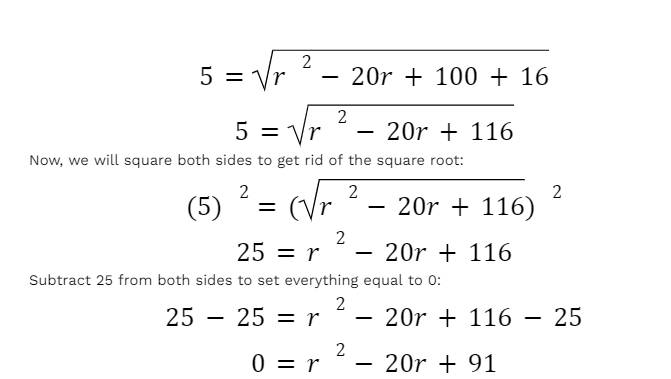
Now, we can factor the equation. First, we will multiply the leading coefficient, 1, and constant, 91, which yields a product of 91. Then, we need to figure out which two numbers have a product of 91 and a sum of -20. This may take some time, but once you have it figured out, you’ll see that -7 and -13 have a product of 91 and a sum of -20. Placing -7r and -13r in place of -20r will give us something like this:

The missing coordinate, r, can either be 7 or 13. Plug both values of r back into the original formula if you would like to check your work. I know this may seem like a lot, but we’re done!
Conclusion
As you learn more, you’ll get better at this, but for now, just continue to practice!
🤝Connect with other students studying Algebra 2 with Hours
Distance Formula and Distance Between Two Points
3 min read•november 23, 2021
Jaaziel Sandoval
Jaaziel Sandoval
Using the Distance Formula and Finding Distance Between Two Points
Introduction to the Distance Formula
Graphs can be a huge pain, especially if you don’t know where to start. The good news is that formulas exist to make life easier! A formula that comes in handy a lot is the distance formula. This formula is derived from the Pythagorean Theorem and is used to find the distance between two points on a graph.
The Formula
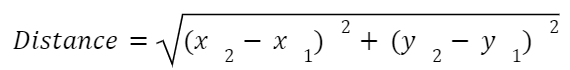
Let’s unpack this formula. x1 , y1refers to the first point you choose and x2 , y2 refers to the second point you choose. Note: It doesn’t matter which point you pick first or second as long as you make sure that you plug them in correctly in the formula! If you’re a bit confused right now, you’ll understand better after doing some practice.
Practice
Find the distance between the two points shown on the graph.

Solution
Choose the red point as x1 , y 1 and the blue point for x2 , y 2. Then, simply plug the coordinates into the distance formula:
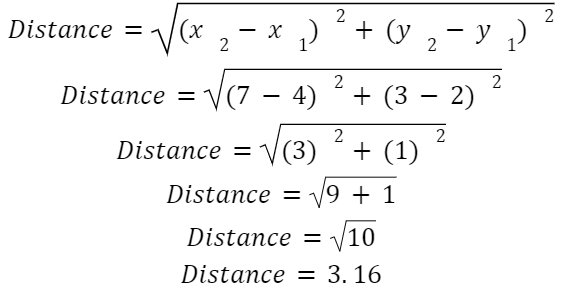
It’s that easy. Remember how it was mentioned that it didn’t matter which point you chose for x1 , y 1 and x2 , y 2? Let’s see why. Choose the blue point as x1 , y 1 and the red point for x2 , y 2 and plug in the coordinates:
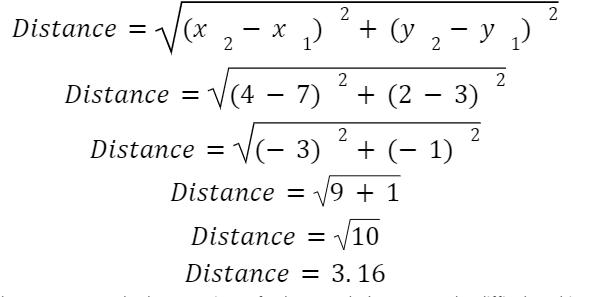
We got the same answer both ways! Piece of cake! Now, let’s ramp up the difficulty a bit. Find the distance between the two points shown on the graph.

Solution
Choose the red point as x1 , y 1 and the blue point for x2 , y 2. Then, simply plug in the coordinates:
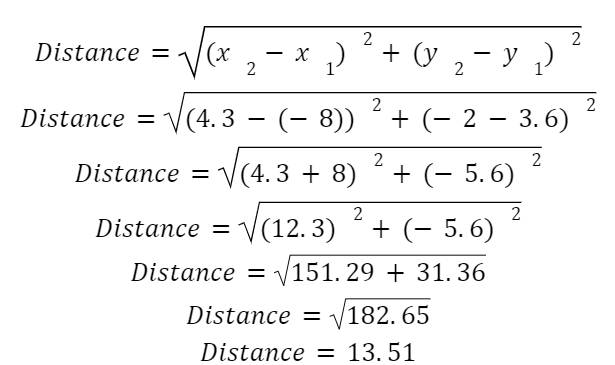
Bam! Easy! Ok, now that we’ve mastered this, let’s spice it up a bit. What happens if you’re given the distance and all of the coordinates except for one. Not to worry, we can just reverse engineer this and get it done. Let’s practice with a word problem instead of a graph this time.
Find the missing point from a line with a distance of 5 and coordinates of (10,7) and (r,3).
Solution
To solve this just plug all the given components, including the unknown variable r, into the formula:
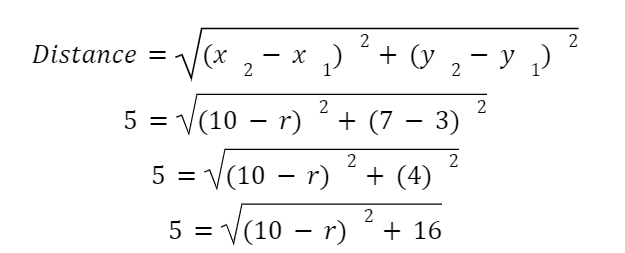
PAUSE! We’ve simplified it as much as we could, now what do we do? We will now expand (10-r)2. If you need help with this or with using the quadratic formula, check out this article from Fiveable. (10-r)2 can be expanded to r2 - 20r + 100, which we can now plug into the formula:
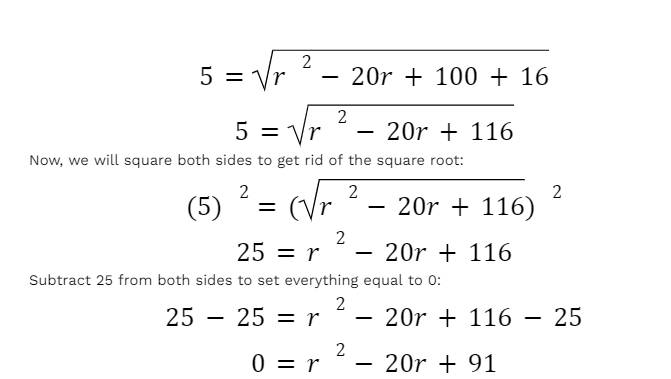
Now, we can factor the equation. First, we will multiply the leading coefficient, 1, and constant, 91, which yields a product of 91. Then, we need to figure out which two numbers have a product of 91 and a sum of -20. This may take some time, but once you have it figured out, you’ll see that -7 and -13 have a product of 91 and a sum of -20. Placing -7r and -13r in place of -20r will give us something like this:

The missing coordinate, r, can either be 7 or 13. Plug both values of r back into the original formula if you would like to check your work. I know this may seem like a lot, but we’re done!
Conclusion
As you learn more, you’ll get better at this, but for now, just continue to practice!
🤝Connect with other students studying Algebra 2 with Hours

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.