2.1 Set Operations and Properties
4 min read•august 12, 2024
Set operations are the building blocks of set theory, allowing us to combine and manipulate sets in various ways. They're crucial for understanding relationships between different groups of elements and solving complex problems in mathematics and computer science.
This section covers basic operations like and , as well as more advanced concepts like power sets and . These tools help us analyze and work with sets efficiently, forming the foundation for more complex set theory applications.
Set Operations
Basic Set Operations
Top images from around the web for Basic Set Operations
Union, Intersection, and Complement | Mathematics for the Liberal Arts View original
Is this image relevant?
Set operations illustrated with Venn diagrams | TikZ example View original
Is this image relevant?
Set language and notation :: Maths View original
Is this image relevant?
Union, Intersection, and Complement | Mathematics for the Liberal Arts View original
Is this image relevant?
Set operations illustrated with Venn diagrams | TikZ example View original
Is this image relevant?
1 of 3
Top images from around the web for Basic Set Operations
Union, Intersection, and Complement | Mathematics for the Liberal Arts View original
Is this image relevant?
Set operations illustrated with Venn diagrams | TikZ example View original
Is this image relevant?
Set language and notation :: Maths View original
Is this image relevant?
Union, Intersection, and Complement | Mathematics for the Liberal Arts View original
Is this image relevant?
Set operations illustrated with Venn diagrams | TikZ example View original
Is this image relevant?
1 of 3
- Union (A ∪ B) combines elements from two sets A and B, creating a new set containing all unique elements from both
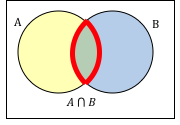
- Intersection (A ∩ B) identifies common elements between two sets A and B, forming a new set with only shared elements
- (A') includes all elements in the that are not in set A
- (A - B) creates a new set with elements from A that are not in B
- (A △ B) produces a set containing elements in either A or B, but not in both
Visualizing Set Operations
- Venn diagrams graphically represent relationships between sets using overlapping circles
- Two-circle Venn diagrams illustrate basic operations like union and intersection
- Three-circle Venn diagrams depict more complex relationships among multiple sets
- Shading in Venn diagrams indicates specific regions corresponding to set operations (union shaded area covers both circles)
Properties of Set Operations
- applies to union and intersection (A ∪ B = B ∪ A, A ∩ B = B ∩ A)
- holds for union and intersection ((A ∪ B) ∪ C = A ∪ (B ∪ C))
- relates union and intersection (A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C))
- exist for union () and intersection (universal set)
- Complement of complement returns the original set (A'' = A)
Set Relationships
Subset and Proper Subset
- (A ⊆ B) indicates every element of A is also an element of B
- (A ⊂ B) means A is a subset of B, but A ≠ B
- Empty set is a subset of all sets
- A set is always a subset of itself
- Subset notation uses symbols ⊆ (subset) and ⊂ (proper subset)
Power Set and Universal Set
- P(A) contains all possible subsets of set A, including the empty set and A itself
- Number of elements in a power set equals 2^n, where n is the number of elements in the original set
- Universal set U encompasses all possible elements under consideration for a given context
- Complement of a set is defined relative to the universal set
- Universal set varies depending on the problem or situation being analyzed
Set Equality and Cardinality
- Two sets are equal if they contain exactly the same elements (A = B if A ⊆ B and B ⊆ A)
- |A| represents the number of elements in set A
- Finite sets have a countable number of elements
- Infinite sets contain an unlimited number of elements (natural numbers, real numbers)
- Cardinality of the power set |P(A)| = 2^|A|
Set Representations and Laws
Set Notation and Representation
- describes sets using a property or rule (A = {x | x is an even number less than 10})
- lists all elements of a set within curly braces (B = {1, 2, 3, 4, 5})
- Empty set represented by {} or ∅
- describes continuous ranges of numbers ([0, 1] represents all real numbers between 0 and 1, inclusive)
De Morgan's Laws
- First law states (A ∪ B)' = A' ∩ B'
- Second law states (A ∩ B)' = A' ∪ B'
- These laws relate complements of unions and intersections
- Useful for simplifying complex set expressions
- Can be extended to more than two sets ((A ∪ B ∪ C)' = A' ∩ B' ∩ C')
Distributive and Other Set Laws
- of union over intersection: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
- Distributive law of intersection over union: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- : A ∪ (A ∩ B) = A and A ∩ (A ∪ B) = A
- : A ∪ A = A and A ∩ A = A
- : A ∪ A' = U and A ∩ A' = ∅
Key Terms to Review (27)
Absorption Laws: Absorption laws are fundamental principles in set theory that describe how certain set operations can simplify expressions involving unions and intersections. These laws state that combining a set with its intersection or union leads to the original set itself, thus demonstrating a kind of redundancy in the operations. They help in understanding how sets relate to each other and simplify complex set expressions.
Associative Property: The associative property refers to a fundamental property of certain binary operations that states the way in which numbers are grouped does not affect their result. This property is significant in operations like addition and multiplication, as it allows the rearrangement of parentheses without changing the outcome. Understanding this property is crucial for simplifying expressions and performing calculations efficiently.
Cardinality: Cardinality refers to the measure of the 'number of elements' in a set, providing a way to compare sizes of both finite and infinite sets. Understanding cardinality is essential in determining whether two sets are equivalent, meaning they have the same number of elements, and it plays a key role in operations like union and intersection. It also leads to insights about countability, distinguishing between different types of infinity.
Commutative Property: The commutative property refers to the fundamental principle in mathematics that states the order of operations does not affect the outcome of certain operations. This property is crucial in understanding how set operations, particularly union and intersection, can be performed regardless of the sequence of the elements involved, leading to consistent results.
Complement: In set theory, the complement of a set A refers to all the elements that are not in A but are part of a universal set U. This concept helps to understand relationships between sets, as it allows for the identification of elements outside of a given subset, facilitating operations like union and intersection. The complement is denoted as A' or U - A and is fundamental in various mathematical contexts, including probability and logic.
Complement Laws: Complement laws are fundamental principles in set theory that describe the relationship between a set and its complement. The laws state that the union of a set and its complement equals the universal set, while the intersection of a set and its complement is an empty set. These laws help clarify how sets interact with one another, highlighting the completeness of the universe of discourse.
De Morgan's Laws: De Morgan's Laws are fundamental rules in logic and set theory that describe the relationship between conjunctions and disjunctions through negation. These laws provide a way to express the negation of logical statements involving 'and' and 'or' by transforming them into equivalent forms. Specifically, they state that the negation of a conjunction is equivalent to the disjunction of the negations, and vice versa, facilitating simplifications in both predicate logic and set operations.
Difference: In set theory, the difference of two sets A and B, denoted as A \ B or A - B, refers to the set of elements that are in set A but not in set B. This operation highlights the distinction between two sets and is crucial for understanding how sets interact with one another, particularly when exploring subsets and complements.
Distributive Law: The distributive law is a fundamental property in mathematics that states how to distribute multiplication over addition or subtraction. Specifically, it indicates that for any numbers or variables a, b, and c, the equation a(b + c) = ab + ac holds true. This principle is essential for simplifying expressions and is widely used in proofs and set operations.
Distributive Property: The distributive property is a fundamental algebraic rule that states that multiplying a number by a sum or difference can be done by multiplying each addend or subtrahend individually and then adding or subtracting the results. This property helps simplify expressions and is crucial for performing operations in set theory, where it applies to unions and intersections. It allows for the breaking down of complex set operations into simpler parts, making calculations easier and clearer.
Empty set: The empty set, denoted as $ ext{∅}$ or `{}`, is a unique set that contains no elements. It is a fundamental concept in set theory and serves as the identity element for set union and the absorbing element for set intersection. Understanding the empty set is essential for grasping the behavior of set operations and the definition of functions involving sets.
Finite Set: A finite set is a collection of distinct elements that contains a limited number of members. This means you can count the elements in the set and determine a specific total, unlike infinite sets, which continue indefinitely. Finite sets are essential in understanding various operations and properties of sets, as well as their cardinality, which refers to the size or number of elements in a set.
Idempotent Laws: Idempotent laws are fundamental properties in set theory that state that applying a set operation multiple times does not change the outcome after the first application. Specifically, for any set A, the union of A with itself is equal to A (i.e., $$A igcup A = A$$), and the intersection of A with itself is also equal to A (i.e., $$A igcap A = A$$). These laws reflect the consistency of operations in set theory and help simplify expressions involving sets.
Identity elements: Identity elements are specific elements in a set that, when combined with any element of that set through a defined operation, leave the other element unchanged. In the context of set operations and properties, identity elements play a crucial role in defining the structure of mathematical operations like union, intersection, and other binary operations within sets.
Infinite set: An infinite set is a collection of elements that does not have a finite number of members. In other words, no matter how many elements you count or list, you can always find more elements to add to the set. This concept is crucial for understanding various properties and operations related to sets, especially when it comes to comparing sizes of different sets and exploring countability, as some infinite sets can be larger than others.
Intersection: The intersection of two or more sets is the set that contains all elements that are common to those sets. This concept plays a crucial role in set operations as it helps to identify shared elements, illustrating relationships between different groups. Understanding intersection is essential for grasping how sets interact and can lead to deeper insights into properties such as subsets and disjoint sets.
Interval Notation: Interval notation is a mathematical way to represent a range of numbers on the number line. It provides a concise format to describe sets of real numbers, indicating whether endpoints are included or excluded, which is crucial for understanding set operations and properties. This notation uses brackets and parentheses to signify closed and open intervals, respectively, linking it directly to concepts of unions, intersections, and complements in set theory.
Power Set: A power set is the set of all possible subsets of a given set, including the empty set and the set itself. The concept of a power set illustrates fundamental properties of sets, as it showcases how set operations can yield new sets while also tying into the idea of functions on sets through mappings that involve subsets. Additionally, understanding power sets is crucial for grasping cardinality, as the size of a power set grows exponentially relative to the original set's size.
Proper Subset: A proper subset is a set that contains some, but not all, elements of another set. This means that if set A is a proper subset of set B, then every element of A is also an element of B, and there exists at least one element in B that is not in A. Proper subsets are crucial for understanding set relationships and operations, particularly when exploring the properties of sets and how they interact with one another.
Roster Notation: Roster notation is a way of specifying a set by listing its elements explicitly within curly braces. This method makes it easy to identify and visualize the members of a set, which is important for understanding set operations and properties, as it allows for quick reference and manipulation of individual elements.
Set Equality: Set equality refers to the concept that two sets are considered equal if they contain exactly the same elements, regardless of the order in which those elements appear or the number of times they appear. This means that for sets A and B to be equal, every element in set A must also be an element of set B and vice versa. Set equality highlights the fundamental property of sets that distinguishes them from other mathematical structures, emphasizing their focus on membership rather than arrangement or frequency.
Set-builder notation: Set-builder notation is a shorthand way of defining a set by specifying a property that its members must satisfy. This notation allows for the concise expression of sets, especially when dealing with infinite or complex sets, by stating conditions that elements must meet to be included in the set. It connects closely with operations and properties of sets, enabling easier manipulation and understanding of their relationships.
Subset: A subset is a set whose elements are all contained within another set. Understanding subsets is crucial because they help in exploring relationships between different sets, allowing us to study how these sets interact and relate to each other in terms of operations like union and intersection, as well as understanding the overall size of sets through concepts like cardinality.
Symmetric difference: The symmetric difference of two sets is the set of elements that are in either of the sets but not in their intersection. It highlights the differences between the two sets and is often denoted as A △ B, where A and B are the two sets being compared. This operation is crucial for understanding how sets relate to each other and is a key aspect of set operations and properties.
Union: In set theory, the union of two or more sets is a new set that contains all the elements from the original sets, without duplication. This operation is fundamental in understanding how different groups of items can be combined and analyzed, making it essential for various mathematical concepts and proofs. The union operation can also be denoted using the symbol '∪', and it has properties that connect it with other operations, like intersection and difference, which help in comprehensively managing sets.
Universal Set: The universal set is the set that contains all possible elements within a particular context or discussion. It serves as the 'big picture' that encompasses all other sets being considered, acting as a reference point for comparisons and operations involving subsets. Understanding the universal set is crucial for operations like unions, intersections, and complements since it establishes the boundaries of what is included in any given analysis.
Venn Diagram: A Venn diagram is a visual representation that illustrates the relationships between different sets. Typically, it consists of overlapping circles, each representing a set, and the intersections of these circles show the elements that are common to the sets. This tool is particularly useful in understanding set operations such as union, intersection, and difference, making it easier to visualize complex relationships among multiple groups.