9.2 Iterative methods for sparse linear systems

Iterative methods are powerful tools for solving large, sparse linear systems efficiently. These techniques generate sequences of improving approximate solutions, leveraging the sparsity of matrices to reduce computational complexity and memory requirements compared to direct methods.

From Jacobi to Gauss-Seidel and beyond, various iterative approaches offer different trade-offs in convergence speed, parallelizability, and memory usage. Understanding their principles, implementation strategies, and performance characteristics is crucial for tackling real-world computational challenges in science and engineering.

Iterative Methods Principles

Fundamentals and Convergence

Top images from around the web for Fundamentals and Convergence

• 

  Gauss-Legendre Iterative Methods and Their Applications on Nonlinear Systems and BVP-ODEs View original

  Is this image relevant?

• 

  An improved statistical iterative algorithm for sparse-view and limited-angle CT image ... View original

  Is this image relevant?

• 

  Gauss-Legendre Iterative Methods and Their Applications on Nonlinear Systems and BVP-ODEs View original

  Is this image relevant?

• 

  An improved statistical iterative algorithm for sparse-view and limited-angle CT image ... View original

  Is this image relevant?

1 of 2

Top images from around the web for Fundamentals and Convergence

• 

  Gauss-Legendre Iterative Methods and Their Applications on Nonlinear Systems and BVP-ODEs View original

  Is this image relevant?

• 

  An improved statistical iterative algorithm for sparse-view and limited-angle CT image ... View original

  Is this image relevant?

• 

  Gauss-Legendre Iterative Methods and Their Applications on Nonlinear Systems and BVP-ODEs View original

  Is this image relevant?

• 

  An improved statistical iterative algorithm for sparse-view and limited-angle CT image ... View original

  Is this image relevant?

1 of 2

• Iterative methods generate sequences of improving approximate solutions for large, sparse linear systems
• General form $x^{(k+1)} = Gx^{(k)} + c$ utilizes iteration matrix G and vector c
• Convergence requires spectral radius of iteration matrix < 1
• Rate of convergence measured by asymptotic convergence factor determines error decrease speed
• Methods classified as stationary (fixed iteration matrix) or non-stationary (adaptive iteration matrix)
• Initial guess $x^{(0)}$ significantly impacts convergence speed and effectiveness
• Preconditioning transforms original system to equivalent system with improved spectral properties for faster convergence

Method Classifications and Techniques

• Stationary methods maintain consistent iteration matrix across all iterations (Jacobi, Gauss-Seidel)
• Non-stationary methods adapt iteration matrix between iterations (Conjugate Gradient, GMRES)
• Splitting techniques decompose coefficient matrix A into simpler components (A = M - N)
  • M chosen for easy inversion
  • N represents remaining terms
• Richardson iteration serves as simple example of stationary method
  • Updates solution using fixed step size along residual direction
• Krylov subspace methods (non-stationary) build solution in expanding subspace
  • Often exhibit faster convergence for certain problem types

Solving Sparse Systems

Classical Iterative Methods

• Jacobi method updates solution components using previous iteration values
  • Easily parallelizable but slower convergence
  • Iteration formula: $x_i^{(k+1)} = \frac{1}{a_{ii}} (b_i - \sum_{j \neq i} a_{ij}x_j^{(k)})$
• Gauss-Seidel method uses most recently computed values for updates
  • Typically faster convergence than Jacobi
  • Iteration formula: $x_i^{(k+1)} = \frac{1}{a_{ii}} (b_i - \sum_{j < i} a_{ij}x_j^{(k+1)} - \sum_{j > i} a_{ij}x_j^{(k)})$
• Successive Over-Relaxation (SOR) introduces relaxation parameter ω
  • Accelerates convergence with 0 < ω < 2
  • ω = 1 reduces to Gauss-Seidel
  • Iteration formula: $x_i^{(k+1)} = (1-\omega)x_i^{(k)} + \frac{\omega}{a_{ii}} (b_i - \sum_{j < i} a_{ij}x_j^{(k+1)} - \sum_{j > i} a_{ij}x_j^{(k)})$

Matrix Splitting and Implementation

• Linear system Ax = b split into A = D - L - U
  • D represents diagonal matrix
  • L represents strictly lower triangular matrix
  • U represents strictly upper triangular matrix
• Iteration matrices derived from splitting determine convergence properties
  • Jacobi: $G_J = D^{-1}(L+U)$
  • Gauss-Seidel: $G_{GS} = (D-L)^{-1}U$
  • SOR: $G_{SOR} = (D-\omega L)^{-1}((1-\omega)D + \omega U)$
• Methods effective for diagonally dominant matrices and certain sparse matrix classes
  • Arise from discretized partial differential equations (finite difference, finite element methods)
• Efficient sparse matrix storage and manipulation crucial for computational advantages
  • Compressed Sparse Row (CSR) format stores non-zero elements and their column indices
  • Compressed Sparse Column (CSC) format stores non-zero elements and their row indices

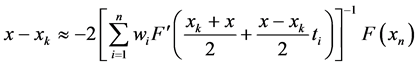
Iterative Method Performance

Convergence Analysis

• Spectral radius of iteration matrix ρ(G) determines convergence rate
  • ρ(G) < 1 ensures convergence
  • Smaller ρ(G) indicates faster convergence
• Asymptotic convergence factor measures error reduction per iteration
  • Defined as $\lim_{k \to \infty} (\frac{||e^{(k+1)}||}{||e^{(k)}||})^{\frac{1}{k}}$
  • e^(k) represents error at k-th iteration
• Number of iterations for desired accuracy influenced by:
  • Condition number of coefficient matrix
  • Initial error magnitude
• Stopping criteria monitor convergence:
  • Relative residual norm: $\frac{||b - Ax^{(k)}||}{||b||}$
  • Absolute error estimates
  • Maximum iteration limits

Method Comparison and Selection

• Computational cost per iteration varies between methods
  • Jacobi requires full vector update each iteration
  • Gauss-Seidel uses immediately updated values, potentially reducing iterations
• Memory requirements differ:
  • Jacobi stores two full solution vectors
  • Gauss-Seidel requires only one solution vector
• Overall time to convergence depends on:
  • Cost per iteration
  • Number of iterations required
• Problem structure impacts method effectiveness
  • Some methods perform better for symmetric positive definite matrices
  • Others excel with non-symmetric or indefinite systems
• Choice between direct and iterative methods considers:
  • Matrix size and sparsity pattern
  • Required solution accuracy
  • Available computational resources
• Advanced techniques (Conjugate Gradient, GMRES) often exhibit faster convergence
  • Particularly effective for certain problem classes
  • May require additional storage or computational overhead

Iterative Methods Implementation

Efficient Data Structures and Algorithms

• Sparse matrix storage formats optimize memory usage and computations
  • Compressed Sparse Row (CSR) stores non-zero elements row-wise
  • Compressed Sparse Column (CSC) stores non-zero elements column-wise
  • Coordinate format (COO) stores row and column indices for each non-zero element
• Vectorization techniques leverage SIMD instructions for improved performance
  • Loop unrolling reduces overhead in iterative computations
  • Cache-friendly data access patterns minimize memory latency
• Parallelization strategies distribute workload across multiple processors
  • Domain decomposition for spatial parallelism
  • Pipeline parallelism for temporal dependencies

Numerical Considerations and Enhancements

• Rounding error accumulation monitored for numerical stability
  • Use of extended precision arithmetic in critical computations
  • Periodic residual recalculation to detect and correct drift
• Ill-conditioned systems require careful treatment
  • Scaling techniques to improve matrix condition number
  • Use of iterative refinement to enhance solution accuracy
• Adaptive strategies improve solver robustness
  • Dynamic selection of relaxation parameters (SOR)
  • Automatic method switching based on convergence behavior
• Preconditioning techniques dramatically improve convergence rates
  • Incomplete LU factorization approximates matrix inverse
  • Algebraic multigrid methods effective for certain problem classes
• Benchmarking against standard test problems evaluates implementation effectiveness
  • Matrix Market collection provides diverse test matrices
  • Comparison with state-of-the-art direct and iterative solvers