11.2 Eulerian and Hamiltonian paths and cycles

Eulerian and Hamiltonian paths and cycles are key concepts in graph theory. They help us understand how we can traverse graphs by visiting edges or vertices. These ideas have real-world applications in network design, route planning, and even DNA sequencing.

While Eulerian paths focus on visiting every edge once, Hamiltonian paths aim to visit every vertex once. Eulerian problems are generally easier to solve, but Hamiltonian problems are more complex. Understanding both helps us tackle various graph-related challenges in computer science and beyond.

Eulerian vs Hamiltonian Paths and Cycles

Definitions and Key Differences

• Eulerian path visits every edge exactly once in a graph
• Eulerian cycle forms a closed path visiting every edge exactly once
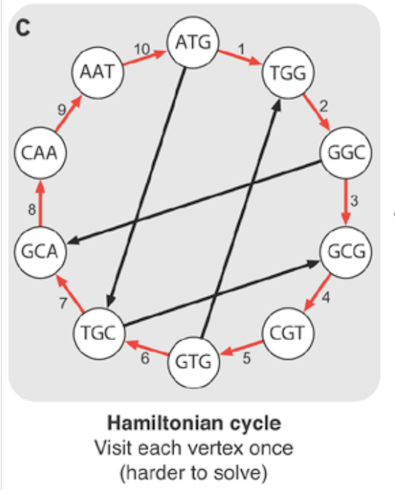
• Hamiltonian path visits every vertex exactly once in a graph
• Hamiltonian cycle forms a closed path visiting every vertex exactly once
• Eulerian concepts focus on edges while Hamiltonian concepts focus on vertices
• Eulerian paths/cycles named after Leonhard Euler who solved Seven Bridges of Königsberg problem (1736)
• Hamiltonian paths/cycles named after William Rowan Hamilton who invented Icosian game (1857)

Complexity and Applications

• Eulerian paths/cycles depend on vertex degrees making them easier to characterize
• Hamiltonian paths/cycles depend on complex structural properties making them NP-complete problems
• Finding Eulerian paths/cycles generally simpler than Hamiltonian counterparts
• Applications include network design (computer networks), optimization problems (delivery routes), and DNA sequencing (genome assembly)

Conditions for Eulerian and Hamiltonian Graphs

Eulerian Path and Cycle Conditions

• Connected graph has Eulerian cycle if all vertices have even degree
• Connected graph has Eulerian path if exactly zero or two vertices have odd degree
  • Two odd-degree vertices serve as start and end points of path
• Directed graphs require strongly connected digraph for Eulerian cycle
  • Every vertex must have equal in-degree and out-degree
• Directed graphs allow Eulerian path under specific degree conditions
  • At most one vertex has (out-degree) - (in-degree) = 1
  • At most one vertex has (in-degree) - (out-degree) = 1
  • All other vertices have equal in-degree and out-degree

Hamiltonian Path and Cycle Conditions

• Necessary condition for Hamiltonian cycle requires connected graph with at least 3 vertices
• Sufficient conditions include Dirac's theorem and Ore's theorem
  • Dirac's theorem states minimum degree ≥ n/2 (n vertices)
  • Ore's theorem requires sum of degrees of non-adjacent vertices ≥ n
• Graph closure concept introduced by Bondy and Chvátal aids in determining Hamiltonicity
  • Involves adding edges between non-adjacent vertices with sufficient degree sum

Finding Eulerian and Hamiltonian Paths

Algorithms for Eulerian Paths and Cycles

• Hierholzer's algorithm efficiently finds Eulerian cycles in undirected graphs
  • Start at any vertex and follow unused edges until returning to start
  • Recursively traverse any remaining circuits
• Fleury's algorithm constructs Eulerian paths/cycles
  • Choose non-bridge edges whenever possible
  • Ensures all edges used exactly once
• Chinese Postman Problem extends Eulerian path finding
  • Solved using matching algorithms for non-Eulerian graphs

Algorithms for Hamiltonian Paths and Cycles

• Depth-First Search (DFS) finds Hamiltonian paths/cycles
  • Worst-case time complexity exponential
• Held-Karp algorithm solves Traveling Salesman Problem
  • Uses dynamic programming
  • Finds minimum-weight Hamiltonian cycle in O(n^2 * 2^n) time
• Approximation algorithms find near-optimal solutions in polynomial time
  • Christofides algorithm for Traveling Salesman Problem
• Heuristic approaches quickly find good Hamiltonian cycles in large graphs
  • Lin-Kernighan heuristic commonly used in practice

Proofs for Eulerian and Hamiltonian Graphs

Eulerian Graph Proofs

• Prove connected graph has Eulerian cycle iff all vertices have even degree
  • Use handshaking lemma and construct cycle
• Demonstrate graph has Eulerian path iff exactly zero or two vertices have odd degree
  • Consider degrees of start and end vertices

Hamiltonian Graph Proofs

• Prove Dirac's theorem for Hamiltonian cycles
  • Show if G has n ≥ 3 vertices and minimum degree δ(G) ≥ n/2, then G Hamiltonian
• Establish Ore's theorem for Hamiltonian cycles
  • Prove if G has n ≥ 3 vertices and d(u) + d(v) ≥ n for non-adjacent vertices u and v, then G Hamiltonian
• Prove Bondy-Chvátal theorem on graph closure and Hamiltonicity
• Demonstrate determining Hamiltonian cycle NP-complete
  • Reduce from 3-SAT problem
• Prove Tutte's theorem that every 4-connected planar graph Hamiltonian
  • Use concept of Tutte cycles