7.1 Principles of dynamic programming
7 min read•august 21, 2024
Dynamic programming is a powerful technique for solving complex optimization problems. It breaks down problems into simpler subproblems, storing solutions to avoid redundant computations. This approach is particularly effective for problems with and .
The method relies on key principles like problem decomposition, state representation, and solution reconstruction. By identifying patterns and relationships between subproblems, dynamic programming can efficiently solve a wide range of combinatorial optimization challenges, from classic problems like knapsack to advanced applications in graph theory and probabilistic modeling.
Fundamentals of dynamic programming
- Optimizes complex problems by breaking them into simpler subproblems
- Stores solutions to subproblems to avoid redundant computations
- Applies to problems with optimal substructure and overlapping subproblems
Optimal substructure principle
Top images from around the web for Optimal substructure principle
Dijkstra's algorithm - Wikipedia View original
Is this image relevant?
Dijkstra's algorithm - Algowiki View original
Is this image relevant?
CS 360: Lecture 22: Single Source Shortest Paths - Dijkstra's Algorithm View original
Is this image relevant?
Dijkstra's algorithm - Wikipedia View original
Is this image relevant?
Dijkstra's algorithm - Algowiki View original
Is this image relevant?
1 of 3
Top images from around the web for Optimal substructure principle
Dijkstra's algorithm - Wikipedia View original
Is this image relevant?
Dijkstra's algorithm - Algowiki View original
Is this image relevant?
CS 360: Lecture 22: Single Source Shortest Paths - Dijkstra's Algorithm View original
Is this image relevant?
Dijkstra's algorithm - Wikipedia View original
Is this image relevant?
Dijkstra's algorithm - Algowiki View original
Is this image relevant?
1 of 3
- Defines problems where optimal solution contains optimal solutions to subproblems
- Allows for recursive problem-solving approach
- Enables efficient solution construction from smaller, solved components
- Applies to problems like shortest path algorithms (Dijkstra's algorithm)
Overlapping subproblems property
- Occurs when a problem can be broken down into subproblems solved multiple times
- Necessitates storing computed results to avoid redundant calculations
- Improves time complexity by trading space for speed
- Manifests in problems like Fibonacci sequence calculation
Memoization vs tabulation
- implements top-down approach, storing results of expensive function calls
- Tabulation uses bottom-up method, solving smaller subproblems first
- Memoization often uses recursion, while tabulation typically employs iteration
- Memoization can be more intuitive, tabulation often more efficient in space usage
- Choice between methods depends on problem structure and implementation preferences
Problem decomposition
- Breaks complex optimization problems into manageable subproblems
- Identifies relationships between subproblems to construct optimal solutions
- Crucial for applying dynamic programming effectively in combinatorial optimization
Subproblem identification
- Involves recognizing smaller, repeated components within the main problem
- Requires understanding problem structure and potential for optimal substructure
- Often begins by solving small instances and identifying patterns
- Includes determining dependencies between subproblems
- Crucial for designing efficient dynamic programming algorithms
Recursive vs iterative approach
- Recursive approach solves problems top-down, often using function calls
- Iterative method builds solutions bottom-up, typically using loops
- Recursive solutions can be more intuitive but may suffer from stack overflow
- Iterative approaches often have better space complexity
- Choice depends on problem structure, language features, and performance requirements
State representation
- Defines how to encode subproblem solutions compactly
- Includes selecting appropriate data structures (arrays, matrices, hash tables)
- Determines efficiency of storage and retrieval of subproblem solutions
- Impacts overall time and space complexity of the algorithm
- May involve techniques like state compression for optimization
Dynamic programming stages
- Outlines the process of developing and implementing dynamic programming solutions
- Provides a structured approach to solving combinatorial optimization problems
- Ensures completeness and correctness of the dynamic programming algorithm
Base case definition
- Establishes simplest subproblems with known solutions
- Serves as the foundation for building more complex solutions
- Often corresponds to trivial or boundary conditions of the problem
- Crucial for terminating recursion in top-down approaches
- Includes identifying and handling edge cases (empty sets, single elements)
Recurrence relation formulation
- Expresses solution to larger problems in terms of smaller subproblems
- Defines how to combine subproblem solutions optimally
- Often involves mathematical equations or logical conditions
- Key to capturing the problem's optimal substructure
- May include multiple cases or conditions depending on problem complexity
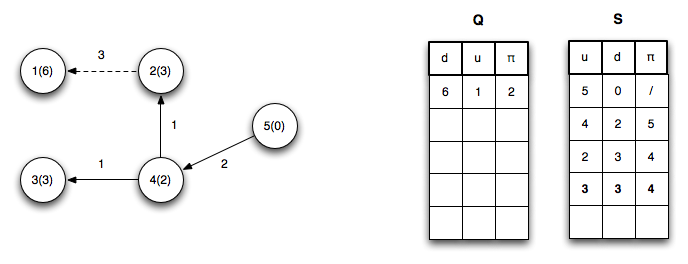
Solution reconstruction
- Traces back through stored subproblem solutions to build the final answer
- Often requires additional data structures to track decisions made
- Involves backtracking from the final state to initial conditions
- Crucial for problems requiring the actual solution, not just its value
- May include techniques like parent pointers or decision matrices
Optimization techniques
- Enhances efficiency and scalability of dynamic programming algorithms
- Crucial for solving large-scale combinatorial optimization problems
- Balances trade-offs between time, space, and implementation complexity
Space complexity reduction
- Utilizes rolling arrays to store only necessary previous states
- Implements in-place updates to reuse memory
- Applies dimension reduction techniques for multi-dimensional problems
- Employs bit manipulation for compact state representation
- Considers trade-offs between space savings and code readability
Time complexity analysis
- Determines runtime efficiency of dynamic programming algorithms
- Involves counting operations in and table filling
- Considers impact of problem size on execution time
- Identifies bottlenecks and opportunities for optimization
- Compares different approaches (recursive vs iterative) for efficiency
Parallelization opportunities
- Identifies independent subproblems suitable for concurrent computation
- Implements parallel algorithms for multi-core or distributed systems
- Considers synchronization and communication overhead in parallel designs
- Applies to problems with non-overlapping subproblems or large state spaces
- Balances potential speedup against increased implementation complexity
Common dynamic programming patterns
- Recognizes recurring structures in dynamic programming problems
- Facilitates problem-solving by applying known strategies to new challenges
- Enhances ability to design efficient algorithms for combinatorial optimization
1D vs 2D dp tables
- 1D tables used for linear dependency problems (coin change, climbing stairs)
- 2D tables applied to problems with two-variable states (edit distance, matrix chain multiplication)
- 1D tables often allow for space optimization through rolling arrays
- 2D tables may require more complex space reduction techniques
- Choice between 1D and 2D depends on problem's state representation needs
Bottom-up vs top-down approaches
- Bottom-up builds solution iteratively from smallest subproblems
- Top-down starts with the main problem and recursively solves subproblems
- Bottom-up often more efficient in terms of constant factors and cache usage
- Top-down allows for lazy evaluation, solving only necessary subproblems
- Implementation choice impacts code structure and optimization opportunities
State compression techniques
- Reduces memory usage by encoding states more efficiently
- Utilizes bit manipulation to pack multiple values into single integers
- Applies hashing techniques to map large state spaces to smaller ones
- Implements rolling hash for string-based dynamic programming problems
- Balances compression benefits against increased computational complexity
Applications in combinatorial optimization
- Demonstrates versatility of dynamic programming in solving complex problems
- Illustrates how theoretical concepts translate to practical algorithm design
- Provides foundation for tackling diverse optimization challenges
Knapsack problem
- Optimizes selection of items with given weights and values to maximize total value
- Uses 2D table to store maximum values for different weights and item subsets
- Applies principle of including or excluding each item based on previous optimal solutions
- Demonstrates trade-off between time complexity and accuracy in pseudo-polynomial solution
- Serves as basis for more complex resource allocation and scheduling problems
Longest common subsequence
- Finds longest sequence of characters appearing in same order in two strings
- Utilizes 2D table to store lengths of common subsequences for prefixes
- Demonstrates optimal substructure in building longer sequences from shorter ones
- Applies to diverse areas (diff tools, bioinformatics sequence alignment)
- Illustrates how dynamic programming can solve problems with multiple input sequences
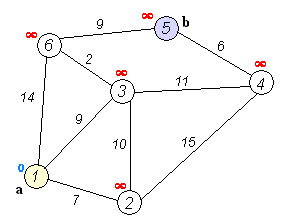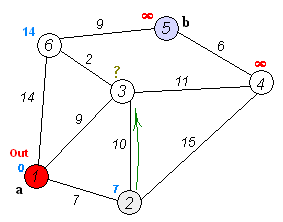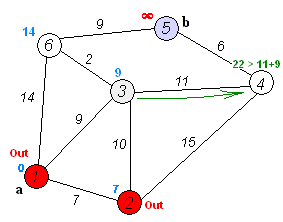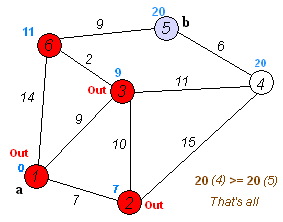
Shortest path problems
- Optimizes routes in weighted graphs to minimize total distance or cost
- Includes algorithms like Floyd-Warshall for all-pairs shortest paths
- Demonstrates how dynamic programming can handle graph-based optimization
- Applies optimal substructure principle in building paths from shorter segments
- Serves as foundation for more complex network optimization problems
Advanced concepts
- Explores sophisticated techniques in dynamic programming
- Extends basic principles to handle more complex problem structures
- Crucial for solving advanced combinatorial optimization challenges
Bitmasking in dynamic programming
- Uses binary representations to efficiently encode and manipulate sets
- Applies to problems involving subsets or permutations (traveling salesman problem)
- Enables compact state representation, reducing space complexity
- Utilizes bitwise operations for fast set operations and state transitions
- Particularly useful for problems with small number of elements but large state space
Multi-dimensional dynamic programming
- Extends DP to problems with more than two state variables
- Applies to complex optimization problems (3D matching, multi-object tracking)
- Requires careful state design to manage increased complexity
- Often involves trade-offs between time, space, and implementation complexity
- May utilize techniques like dimension reduction or state compression for efficiency
Probabilistic dynamic programming
- Incorporates uncertainty and probabilistic outcomes into DP framework
- Applies to stochastic optimization problems (Markov Decision Processes)
- Utilizes expected values and probabilities in recurrence relations
- Extends to areas like reinforcement learning and decision-making under uncertainty
- Requires understanding of probability theory and stochastic processes
Limitations and alternatives
- Recognizes boundaries of dynamic programming applicability
- Explores complementary approaches for problems not suited to pure DP
- Essential for developing comprehensive problem-solving strategies in combinatorial optimization
NP-hard problems
- Identifies optimization problems believed to lack polynomial-time exact solutions
- Includes challenges like traveling salesman problem and graph coloring
- Often requires approximation or heuristic approaches instead of exact DP solutions
- May use dynamic programming as part of more complex solution strategies
- Demonstrates importance of problem classification in algorithm selection
Approximation algorithms
- Provides near-optimal solutions with provable performance guarantees
- Applies to NP-hard problems where exact solutions are infeasible
- May incorporate dynamic programming techniques within approximation schemes
- Includes methods like polynomial-time approximation schemes (PTAS)
- Balances solution quality against computational efficiency
Dynamic programming vs greedy algorithms
- Compares global optimization (DP) with local optimization (greedy) approaches
- DP guarantees but often has higher time/space complexity
- Greedy algorithms make locally optimal choices, may not achieve global optimum
- Some problems (activity selection) allow for both DP and efficient greedy solutions
- Choice depends on problem structure, required optimality, and computational constraints
Key Terms to Review (14)
0/1 knapsack: The 0/1 knapsack problem is a classic optimization problem where the goal is to maximize the total value of items that can be placed into a knapsack of limited capacity. Each item can either be included in the knapsack (1) or excluded (0), leading to the term '0/1'. This problem is significant in dynamic programming as it showcases how optimal solutions can be built from optimal sub-solutions, emphasizing the principle of overlapping subproblems and optimal substructure.
Bellman-Ford Algorithm: The Bellman-Ford algorithm is a dynamic programming algorithm used for finding the shortest path from a single source vertex to all other vertices in a weighted graph. It efficiently handles graphs with negative weight edges and can detect negative weight cycles. This makes it particularly useful in various applications, illustrating principles of dynamic programming, overlapping subproblems, and connections to graph traversal techniques.
Bottom-up approach: The bottom-up approach is a problem-solving strategy that starts from the smallest, simplest components and builds up to solve larger problems, particularly in the context of dynamic programming. This method emphasizes constructing solutions from previously solved subproblems, allowing for efficient computation and minimizing redundancy. By accumulating solutions incrementally, this approach is crucial for optimizing complex problems and provides a systematic way to tackle challenges by leveraging established results.
Feasibility: Feasibility refers to the condition of being achievable or possible within a set of constraints in optimization problems. It determines whether a solution satisfies all the requirements imposed by constraints, ensuring that the solution is not just theoretically optimal but also practically realizable. Understanding feasibility is crucial when working with various problem-solving techniques, as it influences whether a certain approach can lead to a valid solution.
Fibonacci Sequence Algorithm: The Fibonacci Sequence Algorithm is a method for generating the Fibonacci sequence, where each number is the sum of the two preceding ones, usually starting with 0 and 1. This sequence is not only a fascinating mathematical concept but also serves as a classic example of recursive problem-solving, which can be optimized using strategies like memoization. Understanding this algorithm is essential for grasping how recursion can lead to inefficient computations and how dynamic programming can be employed to enhance performance.
Knapsack Problem: The knapsack problem is a classic optimization problem that aims to maximize the total value of items placed into a knapsack without exceeding its capacity. This problem connects to various optimization techniques, as it can be solved using dynamic programming, branch and bound methods, and approximation algorithms, revealing its complexity and practical applications in fields like resource allocation and budgeting.
Longest Common Subsequence: The longest common subsequence (LCS) is a classic problem in computer science that involves finding the longest subsequence that appears in the same relative order in two sequences, but not necessarily consecutively. This concept is fundamental in various applications such as comparing DNA sequences, text comparison, and version control systems. LCS helps in identifying similarities between sequences and can be efficiently solved using dynamic programming techniques.
Memoization: Memoization is an optimization technique used primarily in dynamic programming that involves storing the results of expensive function calls and returning the cached result when the same inputs occur again. This technique helps to avoid redundant calculations, thus improving the efficiency of algorithms that deal with overlapping subproblems. By saving previously computed values, it simplifies problem-solving processes, particularly in recursive algorithms.
Optimal Substructure: Optimal substructure refers to a property of a problem that indicates an optimal solution can be constructed efficiently from optimal solutions of its subproblems. This concept is central in designing algorithms, especially those based on dynamic programming and greedy approaches, where the overall problem can be solved by combining solutions to smaller instances of the same problem.
Optimality: Optimality refers to the state of being the best possible solution to a problem under given constraints. This concept is crucial when evaluating the effectiveness of various problem-solving techniques and algorithms, as it ensures that the selected solution not only addresses the requirements but does so in the most efficient manner. Understanding optimality helps in comparing different approaches, like minimizing cost or maximizing utility, to determine the most effective strategy for achieving desired outcomes.
Overlapping subproblems: Overlapping subproblems refer to a characteristic of certain optimization problems where the same subproblems are solved multiple times during the computation process. This often occurs in recursive algorithms where a problem can be broken down into smaller, similar subproblems that share solutions, leading to redundancy in computation. Recognizing overlapping subproblems is essential for efficient algorithm design, especially when using methods like dynamic programming that leverage previously computed solutions to optimize performance.
Recurrence relations: Recurrence relations are equations that define a sequence of values based on previous terms in that sequence. They serve as a fundamental tool in dynamic programming, as they enable the breakdown of complex problems into simpler, manageable subproblems by expressing the solution to a problem in terms of the solutions to smaller instances of the same problem.
Shortest path problem: The shortest path problem is a classic optimization problem that seeks to find the minimum distance or least-cost path between two nodes in a graph. This problem is essential in various applications, such as routing and navigation, where determining the most efficient route is crucial. The solutions often involve algorithms that utilize optimal substructure, breaking down the problem into smaller subproblems that can be solved independently and combined to form the overall solution.
State transition equations: State transition equations are mathematical formulations used in dynamic programming to describe how the state of a system changes from one time period to another based on decisions made at each step. These equations capture the relationship between current states, decisions, and subsequent states, providing a framework for optimizing sequential decision-making problems. They serve as the backbone of dynamic programming, helping to break down complex problems into simpler subproblems that can be solved systematically.