10.2 Integer Programming
6 min read•july 30, 2024
Integer Programming is a powerful optimization technique that deals with problems where variables must be whole numbers. It's crucial for solving real-world issues like , scheduling, and network design, where fractional solutions don't make sense.
Unlike Linear Programming, Integer Programming handles discrete decisions, making it more challenging to solve. It uses specialized methods like branch-and-bound and cutting planes to find optimal solutions, balancing complexity with practical applications in business and industry.
Linear vs Integer Programming
Continuous vs Discrete Decision Variables
Top images from around the web for Continuous vs Discrete Decision Variables
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
1 of 3
Top images from around the web for Continuous vs Discrete Decision Variables
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
3.2c. Examples: Solving Linear Programming Graphically | Finite Math View original
Is this image relevant?
1 of 3
- Linear programming (LP) problems involve continuous that can take on any real value (0.5, 2.7, etc.), while integer programming (IP) problems require some or all decision variables to be integers (0, 1, 2, etc.)
- LP problems are suitable for modeling decisions that can be divided into fractional parts (allocating resources in continuous quantities), while IP problems are used when decisions are indivisible or require whole units (assigning tasks to workers, selecting projects)
Feasible Region and Solution Methods
- LP problems have a convex feasible region defined by linear constraints, allowing for the use of efficient solution methods like the simplex algorithm
- IP problems, due to the integer restrictions, have a non-convex feasible region, making them more challenging to solve and requiring specialized solution methods (branch-and-bound, cutting planes)
- LP problems can be solved in polynomial time (time complexity grows polynomially with problem size), while IP problems are generally NP-hard (time complexity grows exponentially with problem size)
Real-World Applications
- IP problems arise in various real-world applications where decisions are indivisible or require whole units
- Resource allocation (assigning tasks to machines, workers to shifts)
- Scheduling (job shop scheduling, project scheduling with resource constraints)
- Network design (facility location, supply chain optimization, telecommunication network expansion)
- LP problems are commonly used in applications where continuous decisions are appropriate (blending ingredients in a production process, optimizing investment portfolios)
Formulating Integer Constraints
Decision Variables and Objective Function
- IP problems are formulated using decision variables, an , and constraints, similar to LP problems
- Decision variables in IP problems can be binary (0 or 1), integer (whole numbers), or a combination of both, depending on the problem requirements
- The objective function in IP problems represents the goal to be optimized (minimizing costs, maximizing profits) and is expressed as a linear combination of decision variables
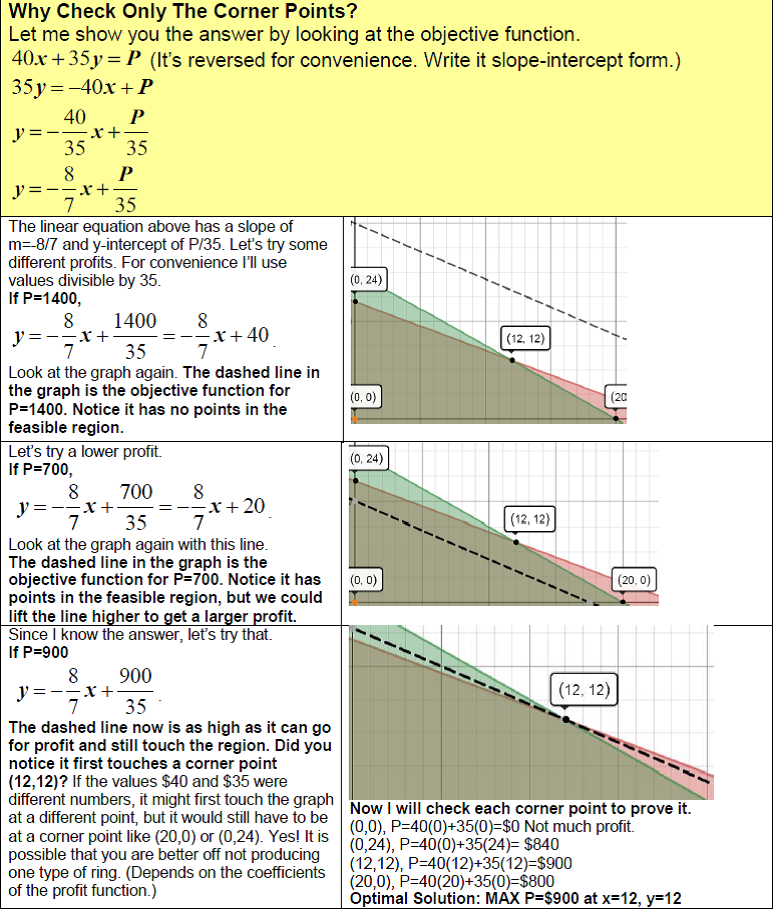
Binary Decision Variables
- Binary decision variables, which can only take values of 0 or 1, are commonly used in IP formulations to represent yes/no decisions or logical conditions
- Selecting projects (1 if project is selected, 0 otherwise)
- Opening facilities (1 if facility is opened, 0 otherwise)
- Binary variables can also be used to model logical constraints, such as "if-then" statements or exclusive choices, by formulating appropriate linear constraints
Integer Decision Variables
- Integer decision variables can represent quantities that must be whole numbers
- Number of products to manufacture
- Number of employees to assign to a task
- Integer variables are used when the problem requires indivisible units or discrete quantities, and fractional solutions are not meaningful or practical
Special Ordered Sets
- IP formulations may also involve (SOS), which are sets of variables where at most one or two variables can be non-zero
- SOS type 1 (SOS1) requires that at most one variable in the set can be non-zero, useful for modeling mutually exclusive decisions (selecting exactly one option from a set of alternatives)
- SOS type 2 (SOS2) allows at most two adjacent variables in the set to be non-zero, useful for modeling piecewise linear functions (approximating nonlinear functions with linear segments)
Solving Integer Programs
Branch-and-Bound Algorithm
- Branch-and-bound is a commonly used exact solution method for IP problems that involves systematically dividing the problem into smaller subproblems and solving them recursively
- The algorithm starts by solving the LP relaxation of the IP problem (ignoring ) and obtaining an upper bound (for maximization problems) or lower bound (for minimization problems) on the optimal objective value
- If the LP solution satisfies the integer constraints, it is optimal for the IP problem; otherwise, the algorithm branches on a fractional variable, creating two subproblems with additional constraints (variable ≤ floor of fractional value, variable ≥ ceiling of fractional value)
- The branch-and-bound algorithm maintains upper and lower bounds on the optimal objective value, allowing for the pruning of subproblems that cannot lead to better solutions, thus reducing the search space
Cutting Plane Methods
- Cutting plane methods iteratively add valid inequalities (cuts) to the LP relaxation of the IP problem, gradually tightening the feasible region until an optimal integer solution is found or the problem becomes infeasible
- Cuts are linear inequalities that are satisfied by all feasible integer solutions but may be violated by the current LP solution, helping to eliminate fractional solutions and improve the LP relaxation
- , derived from the simplex tableau of the LP relaxation, are a well-known class of cutting planes that can be generated algorithmically
- Other types of cuts, such as cover cuts, flow cover cuts, or problem-specific cuts, can be generated based on the structure of the IP problem and the underlying application
Solver Implementations
- Modern IP solvers often employ a combination of branch-and-bound and cutting plane techniques, along with heuristics and preprocessing steps, to efficiently solve large-scale IP problems
- Solvers like , , or SCIP implement advanced algorithms and data structures to handle a wide range of IP problems, exploiting problem structure and using parallel computing to speed up the solution process
- Solver parameters, such as branching strategies, cut generation settings, or heuristic options, can be tuned to improve performance on specific problem instances or application domains
Integer Programming Applications
Resource Allocation and Scheduling
- IP is widely used to model and solve resource allocation problems, such as assigning tasks to machines or workers to shifts
- Binary decision variables represent the assignment of tasks to resources
- Constraints ensure that each task is assigned to exactly one resource and that resource capacities are not exceeded
- , like job shop scheduling or project scheduling with resource constraints, often involve integer decision variables representing start times or sequence positions
- Binary variables can model precedence relationships between tasks
- Integer variables can represent the start time or completion time of each task
- Constraints enforce resource limits and ensure that tasks are scheduled in a feasible order
Network Design and Optimization
- Network design problems, such as facility location, supply chain optimization, or telecommunication network expansion, frequently use binary variables to represent decisions on opening facilities or installing links
- Binary variables indicate whether a facility is opened or a link is installed
- Constraints ensure that demand points are served by open facilities and that flow balance is maintained at each node
- The objective function minimizes the total cost of opening facilities and installing links while satisfying demand
- IP can also be used to solve network flow problems with integer restrictions, such as the minimum cost flow problem with integer flow requirements or the multicommodity flow problem with integer demands
Combinatorial Optimization
- IP is a powerful tool for solving problems, which involve finding an from a finite set of possibilities
- The traveling salesman problem (TSP) can be formulated as an IP problem using binary variables to represent the edges in the tour and subtour elimination constraints to ensure a valid tour
- Vehicle routing problems (VRP) extend the TSP by considering multiple vehicles, capacity constraints, and delivery time windows, and can be modeled using IP with binary variables for vehicle assignments and integer variables for route sequencing
- Graph coloring problems, where the goal is to assign colors to vertices such that no adjacent vertices have the same color, can be formulated as IP problems using binary variables to represent color assignments and constraints to enforce proper coloring
Leveraging Problem-Specific Insights
- In practice, problem-specific knowledge and insights can be leveraged to develop stronger IP formulations, tighten variable bounds, or derive valid inequalities, leading to more efficient solution processes
- Exploiting the structure of the problem, such as symmetries, special constraints, or domain-specific properties, can help reduce the search space and improve solver performance
- Developing customized branching strategies, cut generation routines, or primal heuristics based on the problem characteristics can significantly speed up the solution process and find high-quality solutions more quickly
- Collaborating with domain experts and integrating their insights into the IP formulation and solution approach is crucial for successfully applying IP techniques to real-world problems
Key Terms to Review (20)
Binary integer programming: Binary integer programming is a type of mathematical optimization where the decision variables are restricted to be either 0 or 1. This means that solutions can represent yes/no decisions, making it ideal for problems like resource allocation, scheduling, and facility location where choices are discrete.
Branch and bound: Branch and bound is an algorithmic method for solving integer programming problems, particularly those involving optimization. It systematically explores the solution space by dividing it into smaller subproblems (branching) and using bounds to eliminate subproblems that cannot yield better solutions than the current best (bounding). This approach allows for more efficient searching in complex optimization tasks while ensuring that an optimal solution is found.
Combinatorial Optimization: Combinatorial optimization is a field of mathematical optimization that deals with problems where the objective is to find the best solution from a finite set of possible solutions. This area of study is crucial in various applications, especially in operations research and computer science, where efficient solutions are necessary for complex decision-making problems. It often involves finding optimal arrangements, selections, or combinations under specific constraints.
Constraint formulation: Constraint formulation is the process of defining restrictions or limitations within a mathematical model, particularly in optimization problems. These constraints specify the boundaries within which solutions must be found, ensuring that the results are practical and feasible given real-world conditions. In the context of optimization, constraints can be inequalities or equations that relate to resource availability, time limitations, or other operational factors that must be adhered to.
Cplex: CPLEX is a high-performance mathematical programming solver developed by IBM that is used to solve linear programming (LP), mixed-integer programming (MIP), and quadratic programming (QP) problems. It provides a robust platform for optimizing complex decision-making scenarios, particularly in operations research, logistics, and supply chain management. CPLEX integrates with various programming languages and environments, making it a versatile tool for businesses seeking efficient solutions.
Cutting plane method: The cutting plane method is an algorithmic approach used in mathematical optimization, specifically for solving integer programming problems. This method iteratively refines a feasible region by adding linear constraints, called cutting planes, to eliminate non-integer solutions while maintaining the optimal integer solution. By focusing on the convex hull of feasible integer solutions, the cutting plane method efficiently narrows down the search space to find the best possible solution.
Decision variables: Decision variables are the unknown values that decision-makers need to determine in order to optimize an objective function in mathematical models, particularly in optimization problems. These variables represent the choices available to the decision-maker and are usually subject to constraints that limit their possible values. The optimal values of these decision variables lead to the best possible outcome, whether that's maximizing profit or minimizing cost.
Feasible solution: A feasible solution refers to any solution of a mathematical model that satisfies all the constraints imposed on that model. In the context of optimization problems, particularly integer programming, it’s crucial because only feasible solutions can be considered valid candidates for optimality. Finding a feasible solution is often the first step in solving these types of problems, as it helps to establish a baseline from which further refinements can be made to reach the best possible outcome.
Gomory cuts: Gomory cuts are specific types of cutting planes used in integer programming to refine the feasible region of a linear programming relaxation. These cuts help to eliminate fractional solutions that are not valid for integer constraints, improving the solution space by reducing the area where potential solutions can exist. By adding these constraints, Gomory cuts enhance the performance of optimization algorithms by steering them towards integer solutions more effectively.
Gurobi: Gurobi is a powerful optimization solver designed for solving mathematical programming problems, including linear programming, mixed-integer programming, and quadratic programming. It is widely recognized for its high performance, robustness, and advanced features, making it a popular choice among researchers and practitioners in fields such as operations research, finance, and supply chain management.
Integer Constraints: Integer constraints are restrictions in optimization problems that require some or all of the decision variables to take on integer values. These constraints are essential in scenarios where solutions must represent whole units, such as people, items, or decisions, ensuring that the results of mathematical models are practical and applicable in real-world situations. Integer constraints are commonly used in integer programming to address various business-related problems, including resource allocation and scheduling.
Integrality Gap: The integrality gap is a measure that quantifies the difference between the optimal solution of a linear programming relaxation of an integer programming problem and the optimal integer solution. It reflects how far the solution of the relaxed problem can deviate from the best integer solution, highlighting the challenge of finding efficient solutions in integer programming.
Linear relaxation: Linear relaxation is the process of transforming a mixed-integer programming problem into a linear programming problem by relaxing the integer constraints on the decision variables. This approach allows for continuous variables instead of requiring them to be strictly integer values, which simplifies the problem and makes it easier to solve. Linear relaxation provides an approximation of the optimal solution and is often used as a step in solving integer programming problems, helping identify bounds for the integer solutions.
Mixed-integer programming: Mixed-integer programming (MIP) is a mathematical optimization technique that involves problems where some decision variables are required to take on integer values, while others can be continuous. This approach allows for modeling complex scenarios with both discrete and continuous components, which is essential in various fields like logistics, finance, and manufacturing.
Objective Function: The objective function is a mathematical expression that defines the goal of an optimization problem, typically aiming to maximize or minimize a particular quantity, such as profit, cost, or efficiency. It serves as the core component in various types of optimization models, guiding the decision-making process by indicating the relationship between the variables involved and the desired outcome. The objective function must be constructed based on the specific context and constraints of the problem being addressed.
Optimal solution: An optimal solution refers to the best possible outcome that can be achieved within the constraints of a mathematical model, often maximizing or minimizing a particular objective function. This solution is crucial in decision-making processes as it provides the most efficient use of resources while satisfying all limitations, such as constraints on resources or conditions that must be met.
Polyhedron Theory: Polyhedron theory is a branch of mathematics and optimization that studies the properties and structures of polyhedra, which are solid figures with flat polygonal faces, straight edges, and vertices. This theory plays a crucial role in understanding feasible regions in linear programming, particularly when the solutions must be integers. The relationships between vertices, edges, and faces of polyhedra help in formulating and solving optimization problems efficiently.
Resource Allocation: Resource allocation is the process of distributing available resources among various projects or business units. It involves making decisions on how to best use limited resources, such as time, money, and personnel, to achieve specific goals or objectives. This process is crucial in optimizing performance and ensuring that resources are utilized effectively to maximize returns.
Scheduling problems: Scheduling problems involve the allocation of resources over time to perform a collection of tasks. This concept focuses on optimizing the use of limited resources while minimizing the overall completion time, costs, or conflicts between tasks. The importance of scheduling problems is evident in various fields, including manufacturing, transportation, and project management, where efficient scheduling can lead to significant cost savings and improved operational efficiency.
Special Ordered Sets: Special ordered sets are specific types of variable sets used in integer programming that allow for the modeling of decision-making processes where choices are limited to certain sequences or options. They provide a structured way to handle variables in optimization problems, especially when dealing with binary decisions, by enforcing particular ordering constraints among selected variables.