Glossary

2.3 Boolean functions and normal forms

2 min read•july 24, 2024

Boolean functions form the backbone of digital logic, operating on binary inputs to produce binary outputs. They're represented through truth tables and algebraic expressions, using operators like AND, OR, and NOT to combine variables.

Normal forms, like (DNF) and (CNF), provide standardized ways to express Boolean functions. These forms can be converted between each other and simplified using algebraic manipulation or Karnaugh maps.

Boolean Functions and Normal Forms

Boolean functions and representations

Top images from around the web for Boolean functions and representations

1 of 3

Top images from around the web for Boolean functions and representations

1 of 3

Boolean functions operate on binary inputs (0 and 1) produce binary outputs. Truth tables list all possible input combinations show corresponding for each combination. Algebraic expressions use Boolean operators: AND (⋅\cdot), OR (++), NOT (x‾\overline{x} or x′x') combine variables and operators to form expressions. Common Boolean functions include : f(x,y)=x⋅yf(x,y) = x \cdot y, : f(x,y)=x+yf(x,y) = x + y, : f(x)=x‾f(x) = \overline{x}, and : f(x,y)=x⊕y=xy‾+x‾yf(x,y) = x \oplus y = x\overline{y} + \overline{x}y

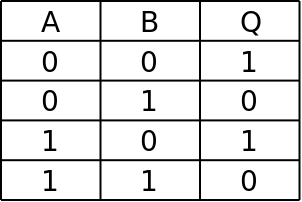
Conversion of normal forms

Disjunctive Normal Form (DNF) represents sum of products as OR of AND terms, each term being a (product of variables or their complements). Conjunctive Normal Form (CNF) represents product of sums as AND of OR terms, each term being a (sum of variables or their complements). Conversion methods include:

  1. From to DNF: Select rows with output 1
  2. From truth table to CNF: Select rows with output 0
  3. DNF to CNF: Use distributive and
  4. CNF to DNF: Use distributive and De Morgan's laws

Simplification of Boolean functions

Algebraic manipulation uses Boolean algebra laws and theorems (commutative, associative, distributive laws) simplifies expressions through factoring and combining terms. Absorption law: x+xy=xx + xy = x and complementation law: x+x‾=1x + \overline{x} = 1 aid in simplification. Karnaugh maps (K-maps) provide two-dimensional grid representation of truth table where adjacent cells differ by one variable. Grouping adjacent 1s or 0s in groups of 2, 4, 8, or 16 cells leads to simpler expressions. Identifying prime implicants and determining essential prime implicants further simplify Boolean functions

Applications in circuit design

Digital circuit design utilizes logic gates (AND, OR, NOT, NAND, NOR, XOR) to create combinational circuits (adders, multiplexers, decoders) and sequential circuits (flip-flops, registers, counters). Control systems implement decision-making algorithms and state machines. Database queries employ Boolean operators in search conditions. Computer architecture applies Boolean functions in instruction set design and memory addressing. Error detection and correction methods use parity bits and Hamming codes. Cryptography incorporates Boolean functions in encryption algorithms. Artificial intelligence leverages Boolean logic in decision trees and rule-based systems

Key Terms to Review (19)

And function: The and function is a fundamental Boolean operation that outputs true only when all of its inputs are true. It plays a crucial role in both the representation of logical expressions and the design of digital circuits, as it combines multiple conditions into a single result, thereby enabling more complex decision-making processes in computing and circuit design.
Associativity: Associativity is a property of certain binary operations that states the way in which operands are grouped in an expression does not affect the result. In algebraic structures, it ensures that when performing operations like addition or multiplication, the order in which operations are performed does not change the outcome, as long as the sequence of the operands remains the same. This property is crucial for understanding the behavior of functions and expressions across various logical systems and is foundational in proving theorems related to logical structures.
Canonical form: Canonical form refers to a standardized way of expressing Boolean functions, enabling easier analysis and comparison. It provides a systematic representation, often in the forms of Sum of Products (SOP) or Product of Sums (POS), which helps in simplifying logical expressions and designing digital circuits. Understanding canonical forms is crucial for tasks like function minimization and algorithm implementation in computer science.
Commutativity: Commutativity is a fundamental property in mathematics that states that the order of operations does not affect the outcome of certain operations. This concept plays a crucial role in various mathematical structures, including algebraic systems, where the ability to rearrange terms without changing the result simplifies expressions and calculations.
Conjunctive Normal Form: Conjunctive Normal Form (CNF) is a way of structuring logical expressions in Boolean algebra, where a formula is represented as a conjunction of one or more clauses, with each clause being a disjunction of literals. This structure makes CNF especially useful in various fields, such as logic programming and satisfiability problems, because it allows for easier manipulation and analysis of complex logical expressions. In particular, CNF plays a critical role in the simplification processes found in algebraic proof theory, the representation of Boolean functions, and database query optimization techniques.
De Morgan's Laws: De Morgan's Laws are fundamental rules in logic and Boolean algebra that describe the relationship between conjunctions (AND) and disjunctions (OR) through negation. These laws state that the negation of a conjunction is equivalent to the disjunction of the negations, and the negation of a disjunction is equivalent to the conjunction of the negations. They play a crucial role in simplifying expressions in Boolean functions and understanding the structure of logical operations.
Digital systems: Digital systems are electronic systems that process, store, and transmit information in a digital format, using discrete values rather than continuous signals. They rely heavily on binary numbers (0s and 1s) to represent data and are foundational in computing and communication technologies. These systems leverage Boolean functions to create logical circuits, which can be represented in various normal forms to optimize performance and functionality.
Disjunctive normal form: Disjunctive normal form (DNF) is a standard way to express a Boolean function as a disjunction of conjunctions, where each conjunction consists of literals. In this format, the function is represented as an OR of ANDs, which helps simplify the analysis and design of logical circuits. This form is crucial for understanding how Boolean functions can be manipulated, making it easier to derive properties and apply them in various logical systems.
Distributive Law: The distributive law states that for any three elements, A, B, and C, the equation A*(B + C) = A*B + A*C holds true. This law is fundamental in both Boolean algebra and classical algebra, enabling the simplification and manipulation of expressions by distributing one operation across another. Its significance spans various fields, connecting logic to algebraic structures, and plays a crucial role in defining normal forms for Boolean functions, circuit design, and applications in database theory.
Evaluation: Evaluation refers to the process of determining the truth value of a Boolean expression or function by substituting its variables with specific values. This is essential in understanding how Boolean functions operate and allows us to analyze the output based on various input combinations. By performing an evaluation, we can also confirm if a Boolean function is in a certain normal form, such as Conjunctive Normal Form (CNF) or Disjunctive Normal Form (DNF).
Karnaugh map: A Karnaugh map is a visual representation of truth tables used to simplify Boolean expressions and functions. It organizes the variables of a Boolean function into a grid format, allowing for easy identification of common patterns and the minimization of logical expressions. This tool is essential for simplifying logic circuits and is widely used in the design of digital electronic systems.
Logic circuits: Logic circuits are electronic circuits that perform logical operations on one or more binary inputs to produce a single binary output. These circuits are foundational to digital computing and are constructed using various components like gates, which implement basic logical functions such as AND, OR, and NOT. Logic circuits can be combined and arranged in numerous ways to create complex systems that can execute a variety of computational tasks.
Maxterm: A maxterm is a specific type of logical expression in Boolean algebra that represents a disjunction of all the variables in a function, each appearing in either true or complemented form. It corresponds to the conditions under which the function evaluates to false, and thus is crucial for constructing canonical forms such as the Sum of Products (SOP). Understanding maxterms helps in converting between different representations of Boolean functions and provides insights into their simplification.
Minterm: A minterm is a specific type of Boolean function that corresponds to a unique combination of variable states in a truth table. It is represented as a product (AND operation) of all the variables in the function, where each variable appears in true or complemented form depending on whether it is assigned a value of 1 or 0, respectively. Minterms are essential for constructing Boolean expressions in canonical form and play a crucial role in simplifying logical expressions.
Not function: A not function, also known as a negation or inverter, is a basic Boolean function that outputs the opposite value of its input. If the input is true (or 1), the output will be false (or 0), and vice versa. This simple yet powerful function is fundamental in constructing more complex logical expressions and circuits, making it essential for understanding how Boolean functions operate and how they can be represented in both normal forms and circuit designs.
Or function: The or function is a fundamental Boolean operation that outputs true if at least one of its inputs is true. It is crucial in logical expressions and circuit design as it allows for decision-making based on multiple conditions, making it a key component in both theoretical and practical applications of Boolean logic. Understanding the or function helps in constructing normal forms of Boolean expressions and designing efficient digital circuits.
Output: In the context of Boolean functions and normal forms, output refers to the result or value produced by a Boolean function based on its input values. This output can be expressed in various forms such as binary digits (0s and 1s), reflecting the true or false evaluations of logical statements. Understanding how outputs are generated from inputs is crucial for analyzing and designing logical expressions and circuits.
Truth table: A truth table is a mathematical table used to determine the truth value of a logical expression based on all possible combinations of truth values for its variables. It provides a systematic way to evaluate how the values of propositions relate to one another and is foundational for understanding logical operations in various fields, such as computer science, mathematics, and circuit design.
Xor function: The xor function, or exclusive OR, is a fundamental Boolean function that outputs true only when exactly one of its inputs is true. This function is essential in the study of logical operations, as it provides a way to model decision-making processes where outcomes depend on distinct conditions. The xor function can be expressed in various forms, including truth tables and algebraic normal forms, making it a key concept in understanding Boolean functions and their applications.
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.
Back
Practice QuizGlossary
Practice QuizGlossary
Next guide