
Determinant of a Matrix
4 min read•december 13, 2021
Amrita A
Amrita A
How to Find The Determinant of a Matrix
What are Matrices?
Matrices are grids of numbers that can represent data or equations. We can use them to represent systems of linear equations by using their coefficients, like the following:
3x - y = 7 and 2x + y = 8 become
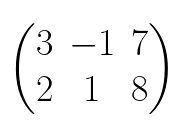
You'll notice throughout this article matrices with different types of brackets: some enclosed in parentheses and others in square brackets. Functionally, it makes no difference which one you use. They're just different notations that certain professions are partial towards.
How Do We Find the Determinant?
Finding the inverse of a matrix can be helpful when you want to get from any matrix to the Identity Matrix, which is the matrix representation of a whole (1):
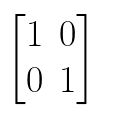
Inverses of Matrices
The inverse of a matrix, usually represented by A⁻¹, is equal to the adjoint of a matrix divided by the determinant. We can find the adjoint of a matrix by switching a and d and making b and c negative in a standard 2x2 matrix:
The inverse of a matrix, usually represented by A⁻¹, is equal to the adjoint of a matrix divided by the determinant. We can find the adjoint of a matrix by switching a and d and making b and c negative in a standard 2x2 matrix:
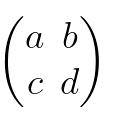
For the inverse of a matrix to exist, it must be a square matrix 🟦. In a square matrix, the number of terms counted vertically must equal the number of terms counted horizontally; in other words, it must be 2x2, 3x3, etc., not 3x2 or 3x4.
When writing down the dimensions of a matrix, the first number represents the number of rows, and the second number represents the number of columns. For example, in a 2x3 matrix, the matrix has 2️⃣rows and 3️⃣columns. In addition, the determinant of the matrix must be greater than 0. So, if you calculate the determinant of a matrix and it equals 0, the inverse of that matrix does not exist ❌
The Determinant of a 2x2 Matrix
Formula
det(A) = |A| = (ad-bc)
The determinant can be represented by “det(A)” or more typically, |A|, with absolute value symbols.
Example Problem
Let’s take a look at the 2x2 matrix in the problem below 🔎
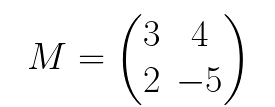
To find the determinant, we must calculate the product of ad and bc. Using the previous abcd matrix, we can say a = 3, b = 4, c = 2, and d = -5. Thus, ad = -15 and bc = 8. If we substitute -15 and 8 for ad and bc in the determinant formula ad-bc, we get (-15 - 8) = -23. Thus, the determinant of this matrix is -23.
The Determinant of a 3x3 Matrix
Formula
|A| = a(ei − fh) − b(di − fg) + c(dh − eg) where
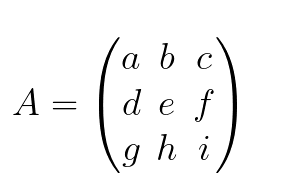
Example Problem
Let’s take a look at the 3x3 matrix supplied in the problem below 🔎
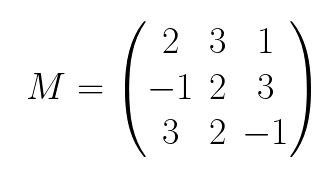
We’ll consider the bottom 6 terms of the matrix as 3 different subcolumns. The formula requires that you multiply a by the determinant of the two rightmost subcolumns (efhi), b by the determinant of the outer two subcolumns (dgfi), and c by the determinant of the two rightmost subcolumns (dgeh).
If we substitute the given matrix’s values into this formula, we have the following 🔢:
|A| = 2(-2-6) - 3(1-9) + 1(-2-6)
|A| = 2(-8) - 3(-8) + 1(-8)
|A| = -16 + 24 -8
|A| = 0
The determinant of Matrix A is 0. This means that its inverse does not exist ❌.
Finding the Determinant on the TI-84
Power on your calculator using the button on the bottom right.
Press the 2nd button, then the X-1 button to get to the matrix menu.
Use the right arrow key to move from NAMES to EDIT.
Use the arrow keys to navigate to the letter you want your matrix to represent and press enter (bottom right of your calculator).
Set the dimensions of your matrix and press the down key after the second dimension to enter the matrix.
Enter your matrix values. Go back to the matrix menu as in Step 2.
Use the right arrow key to navigate from NAMES to MATH.
Choose option 1: "det(" and press enter.
Return to the matrix menu, select the letter of the matrix you chose earlier and press enter.
Close the parentheses and press enter again to get the determinant.
Matrices in Testing
On the ACT, you may need to calculate the product or determinant of a matrix. Check out Fiveable's ACT Math Section Review under our ACT Crams section for more on that!
On the SAT, you may need to add, subtract, multiply, or divide matrices in addition to finding their determinants. Luckily, Fiveable also has resources for SAT Math - see our SAT Crams for more. Overall, general matrix operations are fair game in these standardized tests.
Generally, you can use a test-approved graphing calculator to solve these questions like the TI-84. Matrices may also appear on the Calculus AB test.
Determinant of a Matrix
4 min read•december 13, 2021
Amrita A
Amrita A
How to Find The Determinant of a Matrix
What are Matrices?
Matrices are grids of numbers that can represent data or equations. We can use them to represent systems of linear equations by using their coefficients, like the following:
3x - y = 7 and 2x + y = 8 become
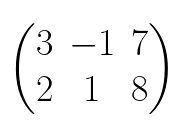
You'll notice throughout this article matrices with different types of brackets: some enclosed in parentheses and others in square brackets. Functionally, it makes no difference which one you use. They're just different notations that certain professions are partial towards.
How Do We Find the Determinant?
Finding the inverse of a matrix can be helpful when you want to get from any matrix to the Identity Matrix, which is the matrix representation of a whole (1):
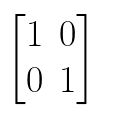
Inverses of Matrices
The inverse of a matrix, usually represented by A⁻¹, is equal to the adjoint of a matrix divided by the determinant. We can find the adjoint of a matrix by switching a and d and making b and c negative in a standard 2x2 matrix:
The inverse of a matrix, usually represented by A⁻¹, is equal to the adjoint of a matrix divided by the determinant. We can find the adjoint of a matrix by switching a and d and making b and c negative in a standard 2x2 matrix:
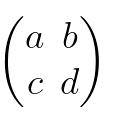
For the inverse of a matrix to exist, it must be a square matrix 🟦. In a square matrix, the number of terms counted vertically must equal the number of terms counted horizontally; in other words, it must be 2x2, 3x3, etc., not 3x2 or 3x4.
When writing down the dimensions of a matrix, the first number represents the number of rows, and the second number represents the number of columns. For example, in a 2x3 matrix, the matrix has 2️⃣rows and 3️⃣columns. In addition, the determinant of the matrix must be greater than 0. So, if you calculate the determinant of a matrix and it equals 0, the inverse of that matrix does not exist ❌
The Determinant of a 2x2 Matrix
Formula
det(A) = |A| = (ad-bc)
The determinant can be represented by “det(A)” or more typically, |A|, with absolute value symbols.
Example Problem
Let’s take a look at the 2x2 matrix in the problem below 🔎
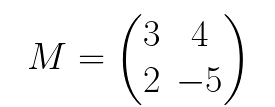
To find the determinant, we must calculate the product of ad and bc. Using the previous abcd matrix, we can say a = 3, b = 4, c = 2, and d = -5. Thus, ad = -15 and bc = 8. If we substitute -15 and 8 for ad and bc in the determinant formula ad-bc, we get (-15 - 8) = -23. Thus, the determinant of this matrix is -23.
The Determinant of a 3x3 Matrix
Formula
|A| = a(ei − fh) − b(di − fg) + c(dh − eg) where
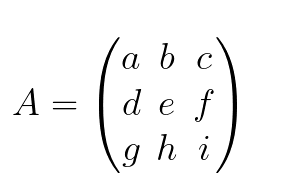
Example Problem
Let’s take a look at the 3x3 matrix supplied in the problem below 🔎
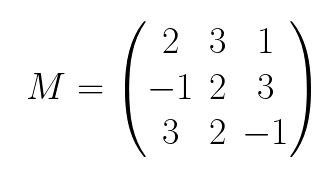
We’ll consider the bottom 6 terms of the matrix as 3 different subcolumns. The formula requires that you multiply a by the determinant of the two rightmost subcolumns (efhi), b by the determinant of the outer two subcolumns (dgfi), and c by the determinant of the two rightmost subcolumns (dgeh).
If we substitute the given matrix’s values into this formula, we have the following 🔢:
|A| = 2(-2-6) - 3(1-9) + 1(-2-6)
|A| = 2(-8) - 3(-8) + 1(-8)
|A| = -16 + 24 -8
|A| = 0
The determinant of Matrix A is 0. This means that its inverse does not exist ❌.
Finding the Determinant on the TI-84
Power on your calculator using the button on the bottom right.
Press the 2nd button, then the X-1 button to get to the matrix menu.
Use the right arrow key to move from NAMES to EDIT.
Use the arrow keys to navigate to the letter you want your matrix to represent and press enter (bottom right of your calculator).
Set the dimensions of your matrix and press the down key after the second dimension to enter the matrix.
Enter your matrix values. Go back to the matrix menu as in Step 2.
Use the right arrow key to navigate from NAMES to MATH.
Choose option 1: "det(" and press enter.
Return to the matrix menu, select the letter of the matrix you chose earlier and press enter.
Close the parentheses and press enter again to get the determinant.
Matrices in Testing
On the ACT, you may need to calculate the product or determinant of a matrix. Check out Fiveable's ACT Math Section Review under our ACT Crams section for more on that!
On the SAT, you may need to add, subtract, multiply, or divide matrices in addition to finding their determinants. Luckily, Fiveable also has resources for SAT Math - see our SAT Crams for more. Overall, general matrix operations are fair game in these standardized tests.
Generally, you can use a test-approved graphing calculator to solve these questions like the TI-84. Matrices may also appear on the Calculus AB test.

Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.