3.1 Eigenvalues and Eigenvectors
4 min read•august 16, 2024
Eigenvalues and eigenvectors are key concepts in matrix theory. They help us understand how matrices transform space, revealing hidden structures and behaviors. This knowledge is crucial for solving complex problems in physics, engineering, and data analysis.
In this section, we'll dive into the math behind eigenvalues and eigenvectors. We'll learn how to calculate them, explore their geometric meaning, and uncover important properties that make them so useful in real-world applications.
Eigenvalues and eigenvectors of matrices
Fundamental concepts
Top images from around the web for Fundamental concepts
Understanding Eigenvalues and Singular Values View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
Understanding Eigenvalues and Singular Values View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
1 of 3
Top images from around the web for Fundamental concepts
Understanding Eigenvalues and Singular Values View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
Understanding Eigenvalues and Singular Values View original
Is this image relevant?
Eigenvalues and eigenvectors - Wikipedia View original
Is this image relevant?
1 of 3
- Eigenvalues (λ) represent scalar values that scale vectors when a matrix is applied to them
- Eigenvectors (v) constitute non-zero vectors that remain in the same direction when multiplied by a matrix
- equation expresses the relationship as , where A represents a square matrix
- Square matrices of size n × n have at most n distinct eigenvalues (real or complex numbers)
- Eigenvalues and eigenvectors apply exclusively to square matrices due to their relation to linear transformations
- refers to the set of all eigenvectors corresponding to a particular eigenvalue
Mathematical properties
- of a matrix equals the sum of its eigenvalues
- of a matrix equals the product of its eigenvalues
- share identical eigenvalues but typically have different eigenvectors
- For any integer k, if λ represents an eigenvalue of A, then λ^k represents an eigenvalue of A^k
- Triangular matrices have eigenvalues located on their main diagonal
- Real symmetric matrices possess real eigenvalues and orthogonal eigenvectors for distinct eigenvalues
- Eigenbasis forms when normalized eigenvectors of a diagonalizable matrix are arranged as columns
Calculating eigenvalues and eigenvectors
Characteristic equation method
- Solve the to find eigenvalues, where I represents the identity matrix
- roots yield the matrix eigenvalues
- For each eigenvalue λ, solve the homogeneous system to determine corresponding eigenvectors
- refers to an eigenvalue's multiplicity as a characteristic polynomial root
- denotes the dimension of an eigenvalue's corresponding eigenspace
- Explicit formulas calculate eigenvalues for 2x2 and 3x3 matrices (quadratic and cubic equations)
- Numerical methods often required for larger matrices (, )
Special cases and simplifications
- Triangular matrices reveal eigenvalues directly on their main diagonal
- Diagonal matrices have eigenvalues equal to their diagonal entries
- Symmetric matrices guarantee real eigenvalues and orthogonal eigenvectors
- Unitary matrices have eigenvalues with magnitude 1
- Nilpotent matrices possess only 0 as an eigenvalue
- Companion matrices have characteristic polynomials equal to their defining polynomials
Geometric interpretation of eigenvalues and eigenvectors
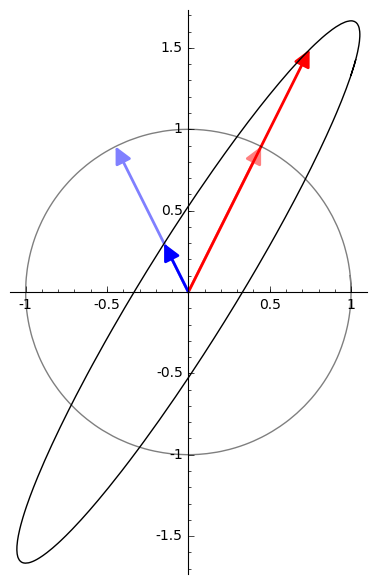
Linear transformations
- Eigenvectors represent directions in which linear transformations scale, rotate, or reflect vectors
- Positive real eigenvalues indicate stretching or compression along the direction (λ > 1 stretching, 0 < λ < 1 compression)
- Negative real eigenvalues represent reflection and scaling along the eigenvector direction
- correspond to rotations combined with scaling in the plane spanned by eigenvector components
- Eigenvalue of 1 signifies unchanged vectors in the corresponding eigenvector direction
- Determinant represents the factor by which the transformation changes volumes (product of eigenvalues)
Visualization in different dimensions
- In 2D: Eigenvectors define invariant lines under the transformation
- Real distinct eigenvalues: Two invariant lines (stretch/compress along each)
- Complex conjugate eigenvalues: Rotation and scaling in the plane
- Repeated eigenvalue: One invariant line, possible shear in perpendicular direction
- In 3D: Eigenvectors with real eigenvalues define of the transformation
- Three real distinct eigenvalues: Three invariant lines
- One real and two complex conjugate eigenvalues: One invariant line and a plane of rotation
- Three repeated eigenvalues: Possible scaling in all directions or more complex behavior
Properties of eigenvalues and eigenvectors
Algebraic relationships
- Sum of eigenvalues equals the trace of the matrix
- Product of eigenvalues equals the determinant of the matrix
- Eigenvalues of matrix powers: If λ represents an eigenvalue of A, then λ^k represents an eigenvalue of A^k
- Eigenvalues of matrix inverses: If λ ≠ 0 represents an eigenvalue of A, then 1/λ represents an eigenvalue of A^(-1)
- Eigenvalues of matrix polynomials: If λ represents an eigenvalue of A, then p(λ) represents an eigenvalue of p(A) for any polynomial p
Structural properties
- Similar matrices (P^(-1)AP) share identical eigenvalues but generally different eigenvectors
- Transpose matrices (A^T) have the same eigenvalues as the original matrix A
- Complex conjugate matrices have complex conjugate eigenvalues
- Hermitian matrices (A^H = A) have real eigenvalues and orthogonal eigenvectors
- Normal matrices (AA^H = A^HA) have orthogonal eigenvectors
- Positive definite matrices have all positive real eigenvalues
Key Terms to Review (24)
Algebraic Multiplicity: Algebraic multiplicity refers to the number of times an eigenvalue appears as a root of the characteristic polynomial of a matrix. It provides important information about the behavior and properties of eigenvalues, indicating how many linearly independent eigenvectors can be associated with that eigenvalue. This concept is crucial in understanding the overall structure and dynamics of linear transformations represented by matrices.
Characteristic Equation: The characteristic equation is a polynomial equation derived from a square matrix that determines the eigenvalues of that matrix. This equation is obtained by subtracting a scalar multiple of the identity matrix from the original matrix and setting the determinant of the resulting matrix to zero. The roots of this polynomial give the eigenvalues, which are essential for understanding the behavior of linear transformations represented by the matrix.
Characteristic Polynomial: The characteristic polynomial of a square matrix is a polynomial that is derived from the determinant of the matrix subtracted by a variable times the identity matrix. This polynomial provides crucial information about the eigenvalues of the matrix, as the roots of the characteristic polynomial correspond to the eigenvalues. Additionally, it encapsulates important properties of the matrix, allowing for analysis in various mathematical contexts, including stability and system dynamics.
Companion Matrix: A companion matrix is a special type of square matrix that represents a polynomial. It is constructed from the coefficients of the polynomial and is used to derive the eigenvalues of that polynomial directly. The eigenvalues of the companion matrix correspond to the roots of the polynomial, making it an essential tool in understanding the relationship between polynomials and their eigenvalues and eigenvectors.
Complex eigenvalues: Complex eigenvalues are values that arise in the context of linear transformations represented by matrices, specifically when the characteristic polynomial has no real roots. These eigenvalues often appear in pairs, along with their corresponding complex eigenvectors, and are particularly important in systems of differential equations and stability analysis. Understanding complex eigenvalues is essential for analyzing the behavior of dynamic systems, especially when they involve oscillations or rotations.
Determinant: The determinant is a scalar value that can be computed from the elements of a square matrix and provides important insights into the properties of that matrix, such as its invertibility and the volume scaling factor for transformations represented by the matrix. It connects to various concepts in linear algebra, including systems of linear equations, eigenvalues, and the LU factorization process, reflecting how a matrix behaves under transformations and its geometric interpretations.
Diagonal Matrix: A diagonal matrix is a special type of square matrix where all elements outside the main diagonal are zero, meaning only the elements on the diagonal (from the top left to the bottom right) can be non-zero. This structure simplifies many matrix operations, such as matrix multiplication and finding eigenvalues, making it easier to work with in various mathematical contexts.
Eigenspace: An eigenspace is a vector space that is associated with a particular eigenvalue of a linear transformation or matrix. It consists of all eigenvectors that correspond to that eigenvalue, along with the zero vector. Understanding eigenspaces helps in analyzing the structure of linear transformations and the behavior of their eigenvectors, which are crucial for various applications in mathematics and engineering.
Eigenvalue: An eigenvalue is a scalar associated with a linear transformation represented by a matrix, indicating how much a corresponding eigenvector is stretched or compressed during that transformation. In simpler terms, if you apply a matrix to an eigenvector, the output is the eigenvector scaled by the eigenvalue. This relationship plays a critical role in many mathematical applications, including stability analysis, systems of differential equations, and understanding the properties of matrices.
Eigenvector: An eigenvector is a non-zero vector that, when multiplied by a given square matrix, results in a scalar multiple of itself. This means that an eigenvector does not change its direction under the transformation defined by the matrix, and it is associated with a specific eigenvalue, which represents the factor by which the eigenvector is scaled. Understanding eigenvectors is crucial for applications such as stability analysis, transformations, and systems of differential equations.
Geometric Multiplicity: Geometric multiplicity refers to the number of linearly independent eigenvectors associated with a particular eigenvalue of a matrix. This concept is crucial in understanding the structure of eigenvalues and their corresponding eigenvectors, as it provides insight into the dimension of the eigenspace linked to that eigenvalue. Geometric multiplicity helps determine whether a matrix can be diagonalized and is always less than or equal to the algebraic multiplicity, which counts the total number of times an eigenvalue appears as a root of the characteristic polynomial.
Hermitian Matrix: A Hermitian matrix is a square matrix that is equal to its own conjugate transpose. This means that the element at position (i, j) in the matrix is the complex conjugate of the element at position (j, i). Hermitian matrices have special properties, such as real eigenvalues and orthogonal eigenvectors, which play a crucial role in various mathematical applications, particularly in linear algebra and quantum mechanics.
Linear Transformation: A linear transformation is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. This means if you take two vectors and add them, or if you multiply a vector by a scalar, the transformation behaves in a way that keeps these operations consistent. Understanding linear transformations is crucial for grasping concepts like eigenvalues and eigenvectors, as they can significantly change the shape and orientation of geometrical representations in vector spaces.
Nilpotent Matrix: A nilpotent matrix is a square matrix $N$ such that there exists a positive integer $k$ for which $N^k = 0$, where $0$ represents the zero matrix of the same size. This property indicates that repeated multiplication of the matrix by itself eventually leads to the zero matrix, highlighting its unique behavior in terms of eigenvalues and eigenvectors, particularly that all eigenvalues are zero.
Normal Matrix: A normal matrix is a type of matrix that commutes with its conjugate transpose, meaning that if \( A \) is a normal matrix, then \( A A^* = A^* A \). This property allows for a number of significant results in linear algebra, particularly regarding eigenvalues and eigenvectors. Normal matrices include special cases such as Hermitian matrices and unitary matrices, which have unique spectral properties that are useful in various applications.
Power Method: The power method is an iterative algorithm used to approximate the dominant eigenvalue and corresponding eigenvector of a matrix. This method starts with an initial vector and repeatedly applies the matrix to this vector, effectively amplifying the influence of the largest eigenvalue while diminishing the effects of smaller ones, allowing convergence to the dominant eigenvector. Its simplicity and effectiveness make it a foundational technique in numerical linear algebra, particularly in contexts where other methods might be impractical due to size or complexity.
Principal Axes: Principal axes are the directions in which a given system's properties, such as inertia or variance, are maximized or minimized. In the context of linear algebra, they are particularly associated with eigenvalues and eigenvectors, where each principal axis corresponds to an eigenvector and is scaled by its corresponding eigenvalue. Understanding principal axes allows for better insight into the geometric transformations and physical interpretations of matrices, especially in applications like data analysis and engineering.
QR Algorithm: The QR algorithm is a numerical method used to compute the eigenvalues and eigenvectors of a matrix by decomposing it into an orthogonal matrix Q and an upper triangular matrix R. This algorithm is significant because it allows for efficient and stable computations in linear algebra, connecting closely with concepts like Schur decomposition and numerical stability.
Real Symmetric Matrix: A real symmetric matrix is a square matrix that is equal to its transpose, meaning that the elements across the main diagonal are mirrored. This property ensures that the matrix has real numbers as its entries and it maintains a certain structure that leads to important results in linear algebra, particularly regarding eigenvalues and eigenvectors.
Similar Matrices: Similar matrices are square matrices that represent the same linear transformation under different bases. Two matrices A and B are considered similar if there exists an invertible matrix P such that $$B = P^{-1}AP$$. This concept connects to eigenvalues and eigenvectors because similar matrices share the same eigenvalues, which means they have the same characteristic polynomial, allowing for deeper insights into their properties through similarity transformations.
Symmetric matrix: A symmetric matrix is a square matrix that is equal to its transpose, meaning that for any matrix \( A \), if \( A = A^T \), then it is symmetric. This property leads to several important characteristics, such as real eigenvalues and orthogonal eigenvectors, which are crucial in various computational methods and applications.
Trace: The trace of a square matrix is the sum of its diagonal elements. This concept is important because it provides insights into the properties of the matrix, such as its eigenvalues and invariants, as it remains unchanged under certain transformations like similarity transformations. Understanding the trace can also aid in various computations related to eigenvalues and their corresponding eigenvectors.
Triangular Matrix: A triangular matrix is a special type of square matrix where all the elements below or above the main diagonal are zero. In the context of linear algebra, triangular matrices simplify the process of solving linear systems and finding eigenvalues and eigenvectors, making them crucial in various computations.
Unitary Matrix: A unitary matrix is a complex square matrix whose conjugate transpose is also its inverse, meaning that if U is a unitary matrix, then $$U^*U = UU^* = I$$, where $$U^*$$ represents the conjugate transpose of U and I is the identity matrix. This property ensures that the rows and columns of a unitary matrix are orthonormal, which is essential in various mathematical concepts such as inner product spaces and quantum mechanics. Unitary matrices preserve norms and angles, making them important in transformations and decompositions in linear algebra.